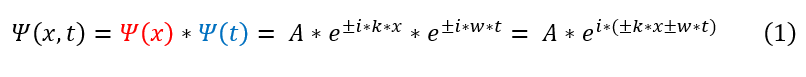Mind Network - Samuel Solomon
Wave-Particle Duality
Wave Function Motivation
It is now the point in time where we may start diving into quantum mechanics. Through rigorous motivation from peculiar experiments and failed attempted models, physicists were stumped at a way to find a solution to the universe. Was light a wave? Was matter a wave? These contradictions were starting to become too difficult to pass off as experimental error. In order to find a solution, a clever little experiment was performed called the double slit experiment.
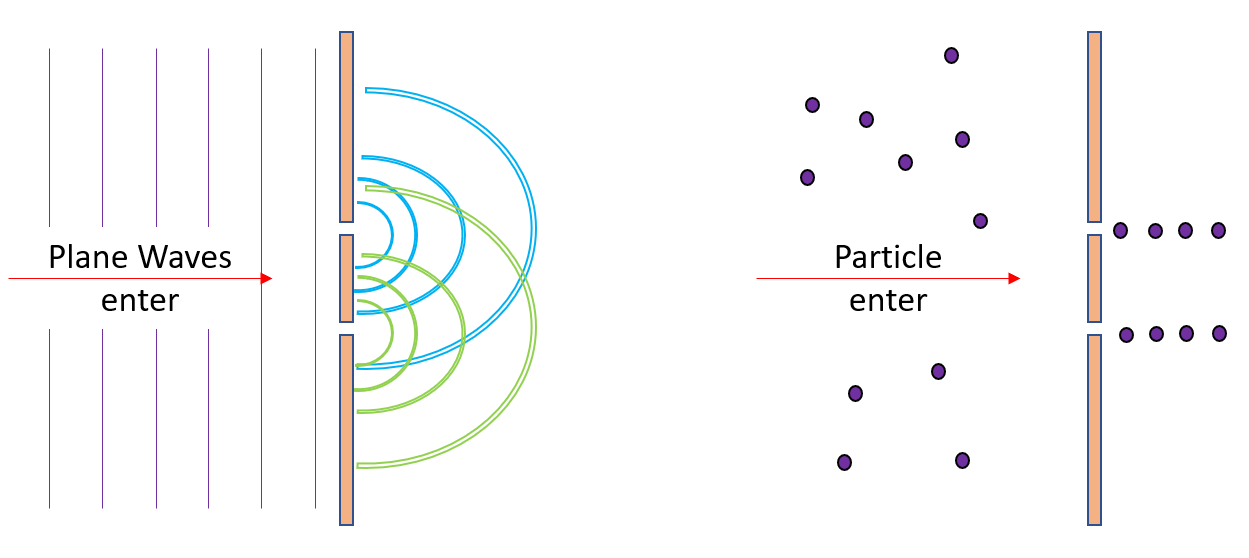
The idea is simple. Water waves show an interference patter as they pass through 2 small slits. This is because one wave will enter both slits at the same time and spread out into each other on the other side. However, particles do not act this way. A particle cannot classically go into both slits at once. This is what the double slit experiment takes advantage of. The idea: shoot particles randomly at 2 slits (one at a time) and see what occurs. With a well-defined solution for each experimental outcome, the experiment seemed promising.
The idea is simple. Water waves show an interference patter as they pass through 2 small slits. This is because one wave will enter both slits at the same time and spread out into each other on the other side. However, particles do not act this way. A particle cannot classically go into both slits at once. This is what the double slit experiment takes advantage of. The idea: shoot particles randomly at 2 slits (one at a time) and see what occurs. With a well-defined solution for each experimental outcome, the experiment seemed promising.
Unfortunately, the results of the double slit experiment are quite unexpected. It can be summarized below:
This experiment back then, and now, makes completely no sense. Shouldn’t the electron have had a defined path the second it left the electron gun? Why is the mere fact that observing the electron forces it into a particle-like behavior. The easy explanation would be that the light (the method we used to observe the electron) changed something about the electron (light does have momentum). It should be noted though that many other different techniques of observing the electron have been tried and re-tried again and again, all of which produce the same results. The crazy idea: the before we see the electron, it has two possible options (for the two open slits). Could it have gone through both and self interfered like a wave?
These slightly philosophical questions lead us to one very important quantum mechanical experimental fact: uncertainty. More on uncertainty will be discussed later, but, for now, understand that the higher wavelength of light used (by the de Broglie relationship h = momentum * wavelength) the lower the momentum of the light. It is only with a low momentum of light (which would produce the least experimental error), but high wavelength, that we do not observe the particle. If we want to observe the particle, we need a small wavelength (smaller than the slit), which means a high momentum of light (and high experimental error). Hence, we have uncertainty in our experiment.
In conclusion, matter cannot be defined as exactly a wave or exactly a particle (both were observed under some conditions), and this should not surprise you. Why should our unseen fundamental makeup of matter be confined to what we can classically see and define as a wave or as a particle? We are so limited by our vision of 3D waves and globular objects. The best guess is that matter probably does not change based on simply observing it, but rather is an entity that has no classical analog of a pure wave or particle. An entity that we can draw relationships to waves and particles, but an entity that is in fact different. It is important to note though, that while I address this fundamental issue, a true physicist is open to all possibilities until affirmatively disproven. So if matter can change based on observation without violating any mathematical or experimental evidence (which it seems so), then that possibility cannot be ignored.
Back to reality, physicists are not patient people. They do not just wait for the universe to give us this particle / wave answer. They look for mathematical models, which we can tweak and refine. To do this, we do need to either favor the wave models or the particle models. Since matter having a defined wavelength was becoming a more reasonable property, the wave function (the solution to the most general wave equation) was used. The wave function is re-shown below:
- 1. If electrons are blindly shot at the slits one at a time, they produced an interference pattern (act like waves)
- By interference pattern, I mean one dot appeared on the detector at a time, but after 10000 or so electrons, the screen looked like a wave passed through (the same locations were hit with the same frequencies)
- 2. If an electron was FIRST OBSERVED to see which of the slits it passed through (one or both), the electron
- produced the expected pattern for a particle (two general peaks; not a wave).
- By observation, I mean light with a wavelength smaller than the slit was shined on the electron to experimentally see at which point in space the electron hit the light (before or after the first slit).
This experiment back then, and now, makes completely no sense. Shouldn’t the electron have had a defined path the second it left the electron gun? Why is the mere fact that observing the electron forces it into a particle-like behavior. The easy explanation would be that the light (the method we used to observe the electron) changed something about the electron (light does have momentum). It should be noted though that many other different techniques of observing the electron have been tried and re-tried again and again, all of which produce the same results. The crazy idea: the before we see the electron, it has two possible options (for the two open slits). Could it have gone through both and self interfered like a wave?
These slightly philosophical questions lead us to one very important quantum mechanical experimental fact: uncertainty. More on uncertainty will be discussed later, but, for now, understand that the higher wavelength of light used (by the de Broglie relationship h = momentum * wavelength) the lower the momentum of the light. It is only with a low momentum of light (which would produce the least experimental error), but high wavelength, that we do not observe the particle. If we want to observe the particle, we need a small wavelength (smaller than the slit), which means a high momentum of light (and high experimental error). Hence, we have uncertainty in our experiment.
In conclusion, matter cannot be defined as exactly a wave or exactly a particle (both were observed under some conditions), and this should not surprise you. Why should our unseen fundamental makeup of matter be confined to what we can classically see and define as a wave or as a particle? We are so limited by our vision of 3D waves and globular objects. The best guess is that matter probably does not change based on simply observing it, but rather is an entity that has no classical analog of a pure wave or particle. An entity that we can draw relationships to waves and particles, but an entity that is in fact different. It is important to note though, that while I address this fundamental issue, a true physicist is open to all possibilities until affirmatively disproven. So if matter can change based on observation without violating any mathematical or experimental evidence (which it seems so), then that possibility cannot be ignored.
Back to reality, physicists are not patient people. They do not just wait for the universe to give us this particle / wave answer. They look for mathematical models, which we can tweak and refine. To do this, we do need to either favor the wave models or the particle models. Since matter having a defined wavelength was becoming a more reasonable property, the wave function (the solution to the most general wave equation) was used. The wave function is re-shown below:
|
|
|