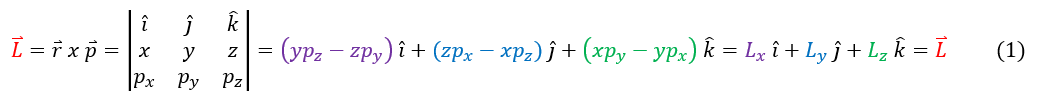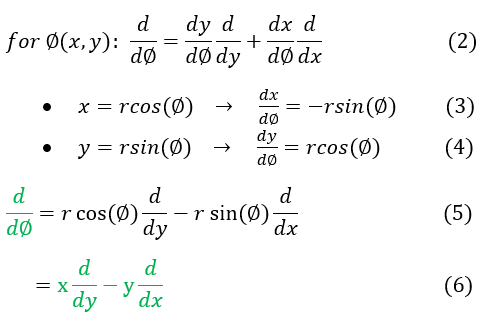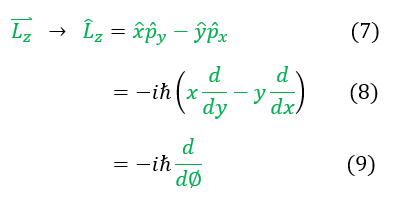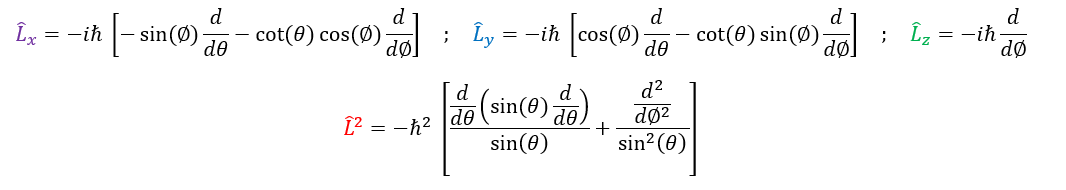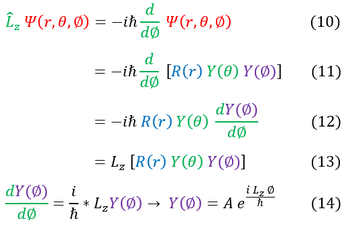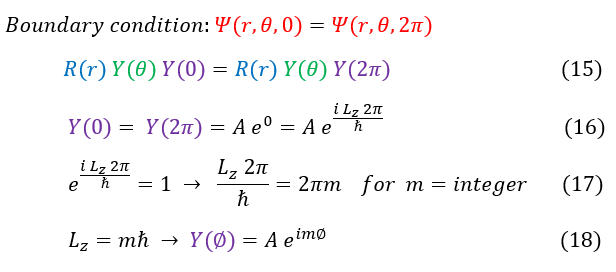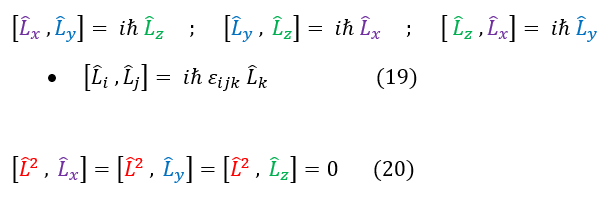Mind Network - Samuel Solomon
Angular Momentum
Operators
|
|
|
Experiments such as the Einstein-De Hass and Stern-Gerlach motivated a new quantum outlook on angular momentum. We know that mathematically it should be a conserved quantity (for no external torque), and that experimentally their seems to be an extrinsic rotational component related to visible gyrations and an intrinsic 'spin' component related to the atoms' dipole (with two quantized 'spin' values).
Analyzing this intrinsic 'spin' component is not very intuitive; hence, we will need to build up our quantum mechanics toolbox just a little more (more information about spin in the course 'quantum mechanics II'). The extrinsic angular momentum, on the other hand, can be visibly and even classically observed. To formulate our quantum operators, let us analyze the classical definition of angular momentum:
Analyzing this intrinsic 'spin' component is not very intuitive; hence, we will need to build up our quantum mechanics toolbox just a little more (more information about spin in the course 'quantum mechanics II'). The extrinsic angular momentum, on the other hand, can be visibly and even classically observed. To formulate our quantum operators, let us analyze the classical definition of angular momentum:
As it turns out, the angular momentum is completely described in terms of the position and momentum (in the x, y, z directions) of the particle. We know the quantum operators of position and momentum and can just substitute them in to find the angular momentum quantum operator.
We will now find the quantum operator of the angular momentum in the 'Z' direction ('L_z'). We will show the direct proof for the z component as it is the most common of the three seen in literature; however, all we are really doing is transforming between Cartesian and spherical coordinates (as you will see; it is more tedious work). We will start on the left with a small relation between spherical and Cartesian derivatives and use it to calculate the z component angular momentum on the right:
We will now find the quantum operator of the angular momentum in the 'Z' direction ('L_z'). We will show the direct proof for the z component as it is the most common of the three seen in literature; however, all we are really doing is transforming between Cartesian and spherical coordinates (as you will see; it is more tedious work). We will start on the left with a small relation between spherical and Cartesian derivatives and use it to calculate the z component angular momentum on the right:
In order to make sure everyone is following, let us review some key steps below:
2: Phi is defined to be the angle in the x-y plane (hence dependent on x and y). In equation 2, we apply the chain rule
3 and 4: We take derivatives of the polar relationships between x, y and phi
5: Plug in the polar relationships found in equations 3 and 4 into equation 2
5 to 6: We can again use the relationships in equations 3 and 4 to get d/dphi in terms of 'x' and 'y'
7: The classical definition of angular momentum (the extrinsic component for quantum mechanics)
7 to 8: Plug in our quantum momentum operator
8 to 9: plug in equation 6 to find the z component angular momentum operator in spherical coordinates
For anyone interested in the other formulas. Through the exact same spherical substitutions, one can find all the spherical angular momentum operators below:
2: Phi is defined to be the angle in the x-y plane (hence dependent on x and y). In equation 2, we apply the chain rule
3 and 4: We take derivatives of the polar relationships between x, y and phi
5: Plug in the polar relationships found in equations 3 and 4 into equation 2
5 to 6: We can again use the relationships in equations 3 and 4 to get d/dphi in terms of 'x' and 'y'
7: The classical definition of angular momentum (the extrinsic component for quantum mechanics)
7 to 8: Plug in our quantum momentum operator
8 to 9: plug in equation 6 to find the z component angular momentum operator in spherical coordinates
For anyone interested in the other formulas. Through the exact same spherical substitutions, one can find all the spherical angular momentum operators below:
Remember, operators are mathematically
defined to scale an eigenfunction by the real observed value. Now that
we have the z component angular momentum operator, we can find the
eigenfunction it acts on to produce the z component angular momentum
eigenvalue:
In order to make sure everyone is following, let us review some key steps below:
10: The L_z operator acting on some unknown eigenfunction
10 to 11: We apply the separation of variables ansatz for a standing wave (for all three variables this time)
11 to 12: The derivative only acts on the Y(phi) function
12 to 13: The operator should scale the whole eigenfunction by some eigenvalue 'L_z' (to be determined)
13 to 14: We set equations 12 and 13 equal to each other and solve for the eigenfunction Y(phi)
We can now apply the boundary condition that phi = 0 is the exact same as phi = 2pi in spherical coordinates (15)
16: Therefore, Y(0) must be equal to Y(2pi). We plug this into our eigenfunction in equation 14
16 to 17: In order for equation 16 to be true, we need the e^ix function to equal 1. e^ix is a sinusoidal function with a
period of 2pi. It starts at 1 where x = 0 and oscillates back every 2pi interval. Hence, when x = 2pi*m (for
some positive or negative integer m), e^ix is ALWAYS equal to 1.
17 to 18: We can now solve for the eigenvalue 'L_z' and, by extension, the eigenfunction Y(phi)
Note that we have solved for a generic z component angular momentum value (hence why we do not get a single angular momentum value, but a range of them for some integer 'm'). What is important to notice is that we have just proven that not all angular momentum values work (it is quantized, just like Bohr predicted).
An additional note is that, while we have not discussed it yet, intrinsic angular momentum can not only have integer values of angular momentum but also half integer values (but that is another story. Just note that you may see h_bar/2 for an m_spin = 1/2). Besides this, intrinsic angular momentum actually follows a lot of the same rules as the extrinsic part (more on that is part II).
Now that we have a great sense of the angular momentum operators, let us evaluate some important commutator relationships between them. Remember, commutators are expressions that allow us to switch the order of two operators as well as tell us information about the two observable's uncertainties (we can know two observables at the same time with certainty if they commute as then they can share a common eigenfunction; see commutator page if confused). Here are some important commutator relationships:
10: The L_z operator acting on some unknown eigenfunction
10 to 11: We apply the separation of variables ansatz for a standing wave (for all three variables this time)
11 to 12: The derivative only acts on the Y(phi) function
12 to 13: The operator should scale the whole eigenfunction by some eigenvalue 'L_z' (to be determined)
13 to 14: We set equations 12 and 13 equal to each other and solve for the eigenfunction Y(phi)
We can now apply the boundary condition that phi = 0 is the exact same as phi = 2pi in spherical coordinates (15)
16: Therefore, Y(0) must be equal to Y(2pi). We plug this into our eigenfunction in equation 14
16 to 17: In order for equation 16 to be true, we need the e^ix function to equal 1. e^ix is a sinusoidal function with a
period of 2pi. It starts at 1 where x = 0 and oscillates back every 2pi interval. Hence, when x = 2pi*m (for
some positive or negative integer m), e^ix is ALWAYS equal to 1.
17 to 18: We can now solve for the eigenvalue 'L_z' and, by extension, the eigenfunction Y(phi)
Note that we have solved for a generic z component angular momentum value (hence why we do not get a single angular momentum value, but a range of them for some integer 'm'). What is important to notice is that we have just proven that not all angular momentum values work (it is quantized, just like Bohr predicted).
An additional note is that, while we have not discussed it yet, intrinsic angular momentum can not only have integer values of angular momentum but also half integer values (but that is another story. Just note that you may see h_bar/2 for an m_spin = 1/2). Besides this, intrinsic angular momentum actually follows a lot of the same rules as the extrinsic part (more on that is part II).
Now that we have a great sense of the angular momentum operators, let us evaluate some important commutator relationships between them. Remember, commutators are expressions that allow us to switch the order of two operators as well as tell us information about the two observable's uncertainties (we can know two observables at the same time with certainty if they commute as then they can share a common eigenfunction; see commutator page if confused). Here are some important commutator relationships:
Let us discuss the importance of these commutators:
Equation 19: As they do not commute, we cannot know for certainty L_x, L_y, or L_z at the same time.
Equation 20: As they do commute, we can know the total angular momentum as well as one of its components at the same time. Their is an eigenfunction shared between the total angular momentum and each of its individual components.
Equation 19: As they do not commute, we cannot know for certainty L_x, L_y, or L_z at the same time.
Equation 20: As they do commute, we can know the total angular momentum as well as one of its components at the same time. Their is an eigenfunction shared between the total angular momentum and each of its individual components.
|
|
|