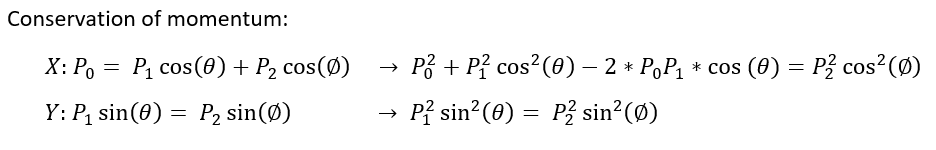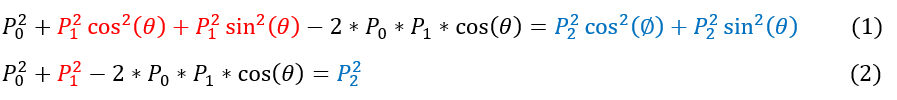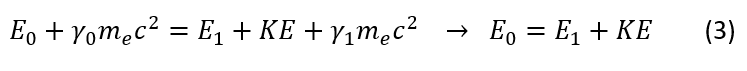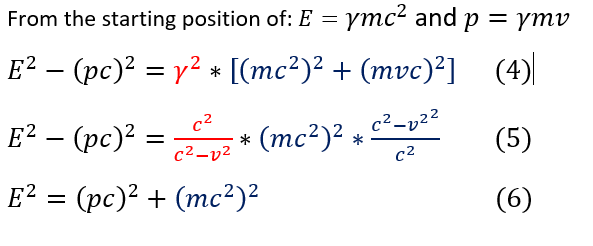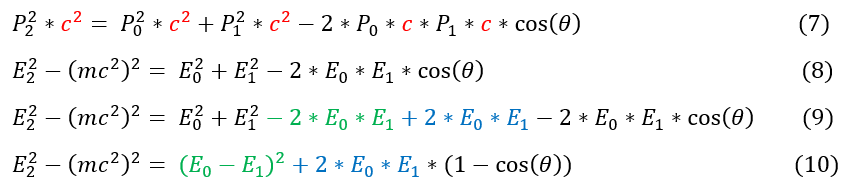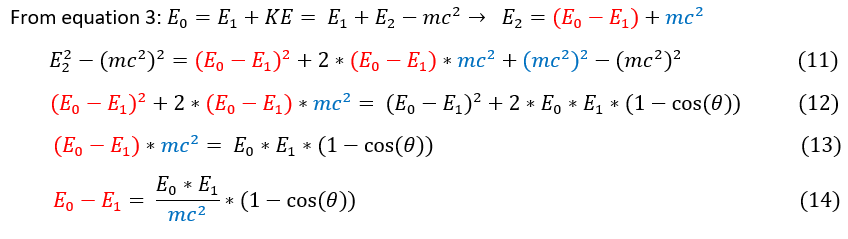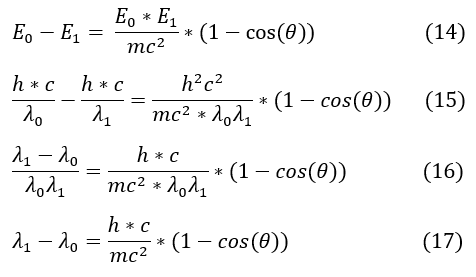Mind Network - Samuel Solomon
Motivation for Quantum Mechanics
Compton Scattering
The photoelectric effect taught us that the energy of light depends on its frequency or wavelength, instead of the number of light particles present. Arthur Holly Compton, a physicist, used this information to explain another problematic experiment: now called the Compton effect.
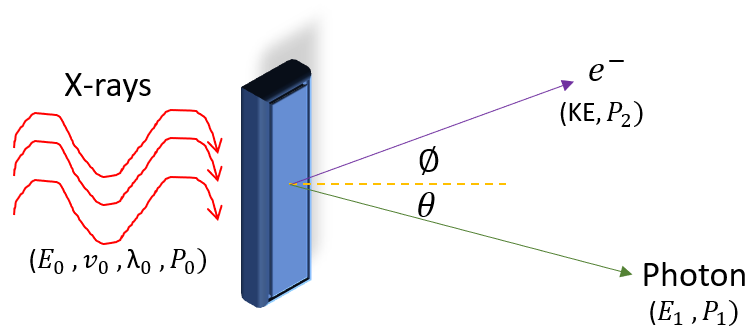
The Compton effect is when electromagnetic radiation (light) scatters of a charged particle (usually a nucleus or an electron). A graphic depiction of the experiment is shown below:
The Compton effect is when electromagnetic radiation (light) scatters of a charged particle (usually a nucleus or an electron). A graphic depiction of the experiment is shown below:
In the experiment, x-rays are shined onto a metal surface (electron rich). It is found that the electron is ejected from the surface at some energy KE and momentum P_2, while the light (which we will now call photons) are scattered off at a different angle with energy E_1 and momentum P_1 (we will talk more about the momentum of light later).
Let us tackle this problem with our conservation laws. Momentum is conserved if no external force acts on our system (F = dp/dt). Energy is conserved if we don't consider mass - energy exchanges (which is reasonable in this experiment, though relativistic effects would add an extra term to our true equation).
Let us tackle this problem with our conservation laws. Momentum is conserved if no external force acts on our system (F = dp/dt). Energy is conserved if we don't consider mass - energy exchanges (which is reasonable in this experiment, though relativistic effects would add an extra term to our true equation).
In order to make sure everyone is following, let us review some key steps below:
We use the conservation of momentum in the x and y direction. For the X momentum, we subtract the P_1 term and square both sides. For the Y momentum, we only square both sides.
We will now add both equations together to get the following:
We use the conservation of momentum in the x and y direction. For the X momentum, we subtract the P_1 term and square both sides. For the Y momentum, we only square both sides.
We will now add both equations together to get the following:
In order to make sure everyone is following, let us review some key steps below:
1 to 2: We use the identity sin^2 + cos^2 = 1
Let us now also consider the conservation of energy:
1 to 2: We use the identity sin^2 + cos^2 = 1
Let us now also consider the conservation of energy:
Please note that I used the relativistic gamma_0 and gamma_1 (called the Lorentz factor) to account for the relativistic energy of the electron. However, since we care more about the significant difference in energy gained by the electron, we will ignore relativistic effects and hence this extra factor (if this factor does not make sense to you, it is okay. I added the relativistic correction for show, but will ignore it for the problem at hand). If one was curious, initially some of the electron's mass is used as binding energy. Once ionized, the electron regains its mass-energy equivalence, which must be accounted for in the conservation of energy equation.
In order to then solve this conservation of energy equation, one must consider what is the energy of a photon? For full generality, we will use the relativistic energy (which came before quantum mechanics) to solve a generic expression for energy. For those not used to relativity, note that all I am using is Einstein's equation E=mc^2 and momentum p =mv where m = mass of the particle. The mass of the particle can be tracked through the Lorentz factor even as the particle speeds up and gains more mass. This is why a gamma factor is added in the equations below.
In order to then solve this conservation of energy equation, one must consider what is the energy of a photon? For full generality, we will use the relativistic energy (which came before quantum mechanics) to solve a generic expression for energy. For those not used to relativity, note that all I am using is Einstein's equation E=mc^2 and momentum p =mv where m = mass of the particle. The mass of the particle can be tracked through the Lorentz factor even as the particle speeds up and gains more mass. This is why a gamma factor is added in the equations below.
In order to make sure everyone is following, let us review some key steps below:
4: Given the two relationships of energy and momentum, E^2 -(pc)^2 was calculated (common expression in relativity)
4 to 5: The true value for gamma is plugged int the red expression and (mc^2)^2 is pulled out of the blue expression.
5 to 6: It is seen that the gamma term cancels, leaving only (mc^2)^2. (pc)^2 is subtracted from both sides.
This equation's importance can be seen once we multiply equation 2 by c^2. Note that the rest mass of a photon is zero (it is thought to be pure energy; at least to the best of our knowledge a photon has momentum and energy, but no mass).
4: Given the two relationships of energy and momentum, E^2 -(pc)^2 was calculated (common expression in relativity)
4 to 5: The true value for gamma is plugged int the red expression and (mc^2)^2 is pulled out of the blue expression.
5 to 6: It is seen that the gamma term cancels, leaving only (mc^2)^2. (pc)^2 is subtracted from both sides.
This equation's importance can be seen once we multiply equation 2 by c^2. Note that the rest mass of a photon is zero (it is thought to be pure energy; at least to the best of our knowledge a photon has momentum and energy, but no mass).
In order to make sure everyone is following, let us review some key steps below:
7 to 8: we replaced (pc)^2 with E^2 - (mc^2)^2 for all p*c. Note, P_0 and P_1 are photons and have no mass.
8 to 9: added and subtracted 2*E_0*E_1 to make 0.
9 to 10: grouped E_0^2 - 2*E_0*E_1 + E_1^2 = (E_0-E_1)^2. Also factored out 2*E_0*E_1 from the remaining terms.
Now that the left hand side looks simplified. Let us turn our eyes to the right hand side. Specifically, let us use the conservation of energy equation 3, replacing the kinetic energy of the electron with the total energy - rest mass energy.
7 to 8: we replaced (pc)^2 with E^2 - (mc^2)^2 for all p*c. Note, P_0 and P_1 are photons and have no mass.
8 to 9: added and subtracted 2*E_0*E_1 to make 0.
9 to 10: grouped E_0^2 - 2*E_0*E_1 + E_1^2 = (E_0-E_1)^2. Also factored out 2*E_0*E_1 from the remaining terms.
Now that the left hand side looks simplified. Let us turn our eyes to the right hand side. Specifically, let us use the conservation of energy equation 3, replacing the kinetic energy of the electron with the total energy - rest mass energy.
In order to make sure everyone is following, let us review some key steps below:
11: After solving for the total energy of the electron E_2, we squared it and put it on the LHS of equation 10
11 to 12: The (mc^2)^2 terms canceled out and the RHS of equation 10 was shown.
12 to 13: Terms on both sides of the equation were canceled out.
13 to 14: E_0 - E_1 (Energy lost by the scattered photon) was found.
Equation 14 is known as the Compton equation. It utilized the notion that light has discrete particle-like qualities such as momentum and accurately accounted for the energy loss of light as it scatters of a charged particle. While Max Plank was the one who first postulated that the energy of a photon = plank's constant (h) * photon frequency (v), the relation was shown here to find the recorded wavelength shift of light as shown below.
11: After solving for the total energy of the electron E_2, we squared it and put it on the LHS of equation 10
11 to 12: The (mc^2)^2 terms canceled out and the RHS of equation 10 was shown.
12 to 13: Terms on both sides of the equation were canceled out.
13 to 14: E_0 - E_1 (Energy lost by the scattered photon) was found.
Equation 14 is known as the Compton equation. It utilized the notion that light has discrete particle-like qualities such as momentum and accurately accounted for the energy loss of light as it scatters of a charged particle. While Max Plank was the one who first postulated that the energy of a photon = plank's constant (h) * photon frequency (v), the relation was shown here to find the recorded wavelength shift of light as shown below.
In order to make sure everyone is following, let us review some key steps below:
14 to 15: We replaced all energy terms with the plank formula for energy E = h*c/wavelength
15 to 16: On the LHS, we combined the 1/ λ_0 - 1/ λ_1 into 1 fraction. h*c was also canceled from both sides
16 to 17: multiplied each side by λ_0* λ_1
14 to 15: We replaced all energy terms with the plank formula for energy E = h*c/wavelength
15 to 16: On the LHS, we combined the 1/ λ_0 - 1/ λ_1 into 1 fraction. h*c was also canceled from both sides
16 to 17: multiplied each side by λ_0* λ_1
|
|
|