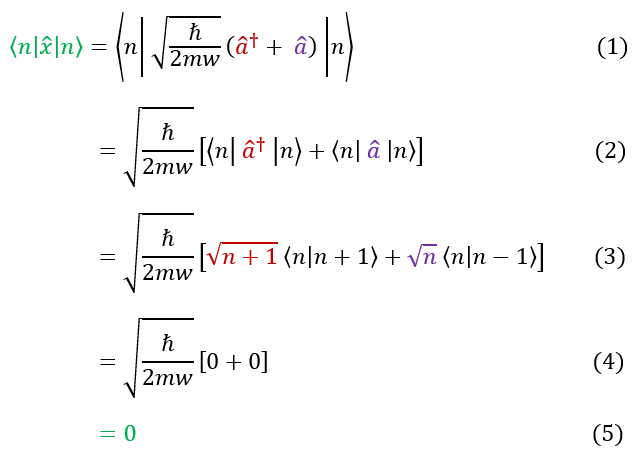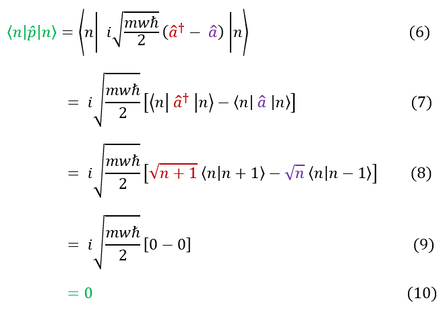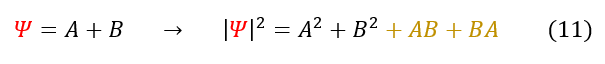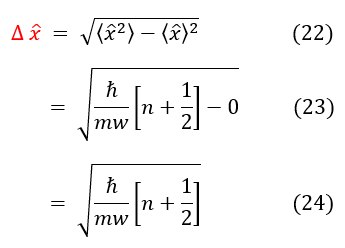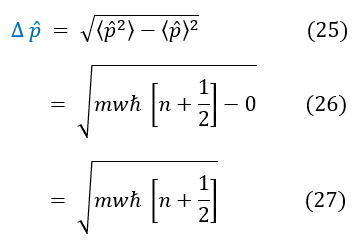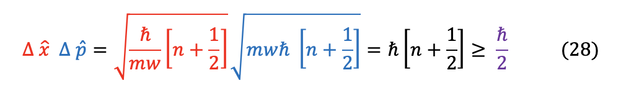Mind Network - Samuel Solomon
Quantum Harmonic Oscillator
Expectation Values
|
|
|
While I could never cover every example of QHOs, I think it is important to understand the mathematical technique in how they are used. To do this, we will solve for the expectation values of x, p, x^2, and p^2 for a wave function in a SINGLE basis state 'n.' Let us start with the x and p values below:
In order to make sure everyone is following, let us review some key steps below:
1: Plug in the ladder operator version of the position operator
1 to 2: Pull out the constant and split the Dirac notation in two
2 to 3: We know how the ladder operators act on QHO states
3 to 4: Each QHO basis state must be orthonormal to each other; zero inner product (no net overlap)
Equations 6 - 10 are the same but for the momentum operator
Hopefully this isn't two shocking of a result. If you have ONE basis state in a symmetric potential well, then the basis state is either even or odd. Mathematically, this means that the total magnitude (amount either negative or positive) of the wave function is the same on both sides of the well. Hence, we should not expect the particle to favor either side (averages to x = 0). Physically, we also note that the particle never gets out of the well, so even though it has some velocity, it must average out to a net velocity of zero (or else it would get out of the well and keep going never to return). Momentum is m*v, so average momentum is zero.
While our classical intuition leads us to the correct answer for the one basis state expectation values, it is important to note that the x and p expectation values are not always zero for the QHO. This is because with two basis states, the waves interfere with each other constructively and destructively. We can no longer think about basis state one and two separately as their is a portion of the probability density that would NEVER have been their if we evaluated the basis waves on their own. You can see this extra term below:
1: Plug in the ladder operator version of the position operator
1 to 2: Pull out the constant and split the Dirac notation in two
2 to 3: We know how the ladder operators act on QHO states
3 to 4: Each QHO basis state must be orthonormal to each other; zero inner product (no net overlap)
Equations 6 - 10 are the same but for the momentum operator
Hopefully this isn't two shocking of a result. If you have ONE basis state in a symmetric potential well, then the basis state is either even or odd. Mathematically, this means that the total magnitude (amount either negative or positive) of the wave function is the same on both sides of the well. Hence, we should not expect the particle to favor either side (averages to x = 0). Physically, we also note that the particle never gets out of the well, so even though it has some velocity, it must average out to a net velocity of zero (or else it would get out of the well and keep going never to return). Momentum is m*v, so average momentum is zero.
While our classical intuition leads us to the correct answer for the one basis state expectation values, it is important to note that the x and p expectation values are not always zero for the QHO. This is because with two basis states, the waves interfere with each other constructively and destructively. We can no longer think about basis state one and two separately as their is a portion of the probability density that would NEVER have been their if we evaluated the basis waves on their own. You can see this extra term below:
The yellow term would not normally be their if we only considered the probabilities of A and B separately. The fact that they are in 1 combined wave function changes the math just enough for our classical intuition to be mixed up.
Let us now move onto the expectation values for x^2 and p^2 for ONE basis state:
Let us now move onto the expectation values for x^2 and p^2 for ONE basis state:
In order to make sure everyone is following, let us review some key steps below:
12: Plug in the ladder operator version of the position operator (in the QHO state)
12 to 13: Pull out the constant and distribute the ladder operators
13 to 14 We know how the ladder operators act on QHO states (plug in the eigenvalues)
14 to 15: Each QHO basis state must be orthonormal to each other; zero inner product (no net overlap)
15 to 16: Simplify the expression
Equations 17 - 21 follows the exact same logic, but now with momentum
A last check to make sure nothing is sketchy is to calculate the uncertainty in x and p:
12: Plug in the ladder operator version of the position operator (in the QHO state)
12 to 13: Pull out the constant and distribute the ladder operators
13 to 14 We know how the ladder operators act on QHO states (plug in the eigenvalues)
14 to 15: Each QHO basis state must be orthonormal to each other; zero inner product (no net overlap)
15 to 16: Simplify the expression
Equations 17 - 21 follows the exact same logic, but now with momentum
A last check to make sure nothing is sketchy is to calculate the uncertainty in x and p:
It checks that Heisenberg's uncertainty principle holds for every nth excited state of the QHO, so we are not in violation of any known principles.
|
|
|