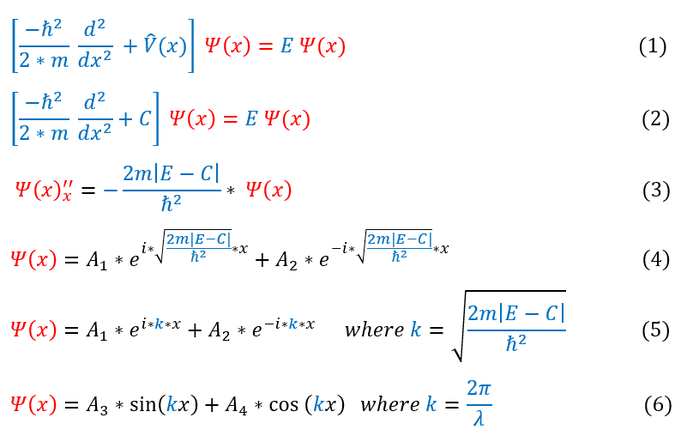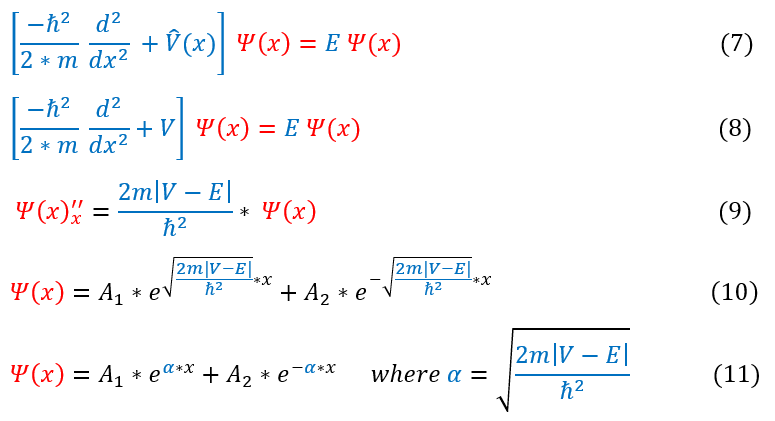Mind Network - Samuel Solomon
Bound States
The Mathematical Setup
The infinite square well assumes that an electron (particle) is fixed in a bounded region, with zero probability of escaping the region. This assumption arose entirely out of setting the potential to infinity outside the box. While this is a theoretical situation in certain limits (extremes), we can indeed define potentials numerically (big, but finite numbers).
For our finite potential, we will first claim that the particle's energy will always be less than the finite potential. We call these types of situations “bound states” or “finite potential wells” as the particle is still bounded by a potential barrier (theoretically cannot climb over). A real-life version of a bound state is a reaction without enough energy to proceed. The molecule does not have enough energy to surmount the potential barrier (called activation energy) to access a configuration or speed necessary for a reaction, but enough energy to exist in whatever starting conformation it takes. We will further discuss this example later in the course (when we build up enough principles to discuss quantum tunneling).
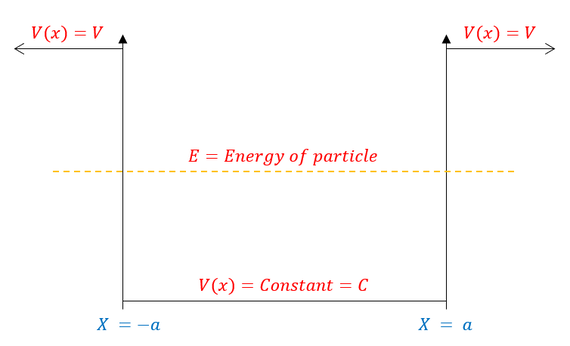
An energy diagram visually depicting the bound state I described can be seen below:
For our finite potential, we will first claim that the particle's energy will always be less than the finite potential. We call these types of situations “bound states” or “finite potential wells” as the particle is still bounded by a potential barrier (theoretically cannot climb over). A real-life version of a bound state is a reaction without enough energy to proceed. The molecule does not have enough energy to surmount the potential barrier (called activation energy) to access a configuration or speed necessary for a reaction, but enough energy to exist in whatever starting conformation it takes. We will further discuss this example later in the course (when we build up enough principles to discuss quantum tunneling).
An energy diagram visually depicting the bound state I described can be seen below:
In the figure above, we center the ‘potential energy box’ around x = 0. We keep generality by labeling the bottom of the well with a potential of 'C' (not zero, as we did earlier). This generality matters as while there is no real difference between infinity and a constant vs infinity and zero, there is a mathematical difference between a constant and a non-zero number vs a constant and zero (ie it didn't matter in the infinite well, but it does matter in the finite well).
Just like for the infinite potential well, we can now break up the problem into different regions. Let us start our analysis by looking at the region inside the box. We call this region the classically allowed region because it intuitively made sense to exist before quantum mechanics. If I shoot a ball up into the air with more energy than the potential energy of a hoop (V = mgh), then the ball with go above the hoop. If I smash my hand into a wall with more energy than the intermolecular bonds holding the wall together, my hand will go through the wall. If I have more energy than a system, I can expect to pass it (with some distribution of failed attempts). I would not expect to occupy a space where the repulsion energy (the barrier to exist in) is greater than the energy I have. We saw this in the infinite square well when psi(x) went to zero as the potential energy grew too high.
With this classical intuition, let us now listen to what the math has to say:
Just like for the infinite potential well, we can now break up the problem into different regions. Let us start our analysis by looking at the region inside the box. We call this region the classically allowed region because it intuitively made sense to exist before quantum mechanics. If I shoot a ball up into the air with more energy than the potential energy of a hoop (V = mgh), then the ball with go above the hoop. If I smash my hand into a wall with more energy than the intermolecular bonds holding the wall together, my hand will go through the wall. If I have more energy than a system, I can expect to pass it (with some distribution of failed attempts). I would not expect to occupy a space where the repulsion energy (the barrier to exist in) is greater than the energy I have. We saw this in the infinite square well when psi(x) went to zero as the potential energy grew too high.
With this classical intuition, let us now listen to what the math has to say:
. In order to make sure everyone is following, let us review some key steps below:
1: The time independent Schrödinger equation
1 to 2: Replacing V(x) for 'C' for the region inside the box
2 to 3: Pushing all the constants onto one side. 'E' is always bigger than 'C' in this case (wrote in absolute value form)
3 to 4: Solving the differential equation (there are always 2 solutions for a second derivative equation)
4 to 5: Replacing the constants in the exponent with the value 'k'
5 to 6: e^ikx describe sinusoidal functions based on Euler's formula (e^ikx = sin(kx)+i*cos(kx)). From wave mechanics,
we can mathematically interpret the 'k' value as the wave number of the oscillating wave (λ= wavelength)
We can note a couple important principles about equations 4-6:
1. When the energy 'E' is greater than the potential 'C', the solution is an oscillatory function.
If 'k' is real then e^ikx is oscillatory as shown above, but if 'k' was imaginary, e^ikx would be e^-|k|x (exponential)
2. A greater energy-potential gap 'E-C' = higher k-value = lower wavelength of wave = higher frequency
This makes sense as E = h*v, so a higher frequency means a higher energy for the same potential
Let us now turn our attention to the outer two regions where the potential barrier is too great for the particle's energy. We call this region the classically forbidden region because the particle should never occupy this space. If I shoot a ball up into the air with less energy than the potential energy of a hoop (V = mgh), then the ball should not go above the hoop. If I smash my hand into a wall with less energy than the intermolecular bonds holding the wall together, my hand should not go through the wall. If I have less energy than a system, I cannot occupy its space.
Let us now take a look at the math for this region:
1: The time independent Schrödinger equation
1 to 2: Replacing V(x) for 'C' for the region inside the box
2 to 3: Pushing all the constants onto one side. 'E' is always bigger than 'C' in this case (wrote in absolute value form)
3 to 4: Solving the differential equation (there are always 2 solutions for a second derivative equation)
4 to 5: Replacing the constants in the exponent with the value 'k'
5 to 6: e^ikx describe sinusoidal functions based on Euler's formula (e^ikx = sin(kx)+i*cos(kx)). From wave mechanics,
we can mathematically interpret the 'k' value as the wave number of the oscillating wave (λ= wavelength)
We can note a couple important principles about equations 4-6:
1. When the energy 'E' is greater than the potential 'C', the solution is an oscillatory function.
If 'k' is real then e^ikx is oscillatory as shown above, but if 'k' was imaginary, e^ikx would be e^-|k|x (exponential)
2. A greater energy-potential gap 'E-C' = higher k-value = lower wavelength of wave = higher frequency
This makes sense as E = h*v, so a higher frequency means a higher energy for the same potential
Let us now turn our attention to the outer two regions where the potential barrier is too great for the particle's energy. We call this region the classically forbidden region because the particle should never occupy this space. If I shoot a ball up into the air with less energy than the potential energy of a hoop (V = mgh), then the ball should not go above the hoop. If I smash my hand into a wall with less energy than the intermolecular bonds holding the wall together, my hand should not go through the wall. If I have less energy than a system, I cannot occupy its space.
Let us now take a look at the math for this region:
We follow the same math as before, but now the potential is greater than 'E' and hence we differ by a negative sign. From a differential equation standpoint, this negative sign is extremely important as now the solution is not a sinusoidal function, but an exponential function, specifically an exponential increase or decrease. We call these specific functions hyperbolic (as they related to hyperbolic cosine and sin).
We can note a very important principle about equations 10-11:
1. When the energy 'E' is less than the potential 'V', the wave function is made of exponential hyperbolic functions.
The lower the energy is (the bigger the energy-potential gap is) the faster the function exponentially decays. This makes intuitive sense because we logically didn’t even assume that the particle could even exist in this region. Obviously, the higher the activation energy (the gap) is, the harder it would be for the particle to somehow reach this position.
This is also coherent with our mathematical finding from the infinite square well. The infinite square well is just the finite square well with a HUGE energy-potential gap. We found that in this specific limit, the particle mathematically disappears. We approximately see this in the finite potential well as the wave function goes to zero exponentially fast as the potential goes to infinity (the function exponentially decays so fast that it barely even penetrates the potential barrier at all).
BUT WAIT: some of the people following along may be starting to connect some of the dots as to why this result is so troubling. Psi(x) is the time independent form of the wave function. The wave function squared relates to the probability of finding a particle in a given space. If there exists some wave function in a classically forbidden region, then so does there exist some probability of a particle occupying a space it never should. There is a probability of you falling through the floor, your goldfish swimming out of its tank, and your hat falling through your head. And this probability is quantifiable and experimentally proven to exist.
Takeaway from bound states:
The fact that a particle can be in a place where it does not have enough energy to occupy is VERY significant and shocking. One can see this in a quick example: a ball is thrown against. When thrown, the ball has enough energy to travel through the air. If supplied even more energy, greater than the wall's potential barrier, the ball can travel through the wall (we will call that scattering, but more on that later). In contrast, if the ball does not have enough energy, we would not expect it to go through the wall and rather stop at the wall or bounce back. However, we just proved that according to quantum mechanics there is a possibility, even without enough energy, for the ball to enter the wall’s space (and no we are not talking about deforming the wall; actually, enter the wall). Let me quickly note that real numerical examples show this to be very unlikely, but it is possible. In fact, physicists have used this principle to push reactions forwards without (though usually close to) the necessary energy. We call this potential barrier penetration ‘quantum tunneling.’
We can note a very important principle about equations 10-11:
1. When the energy 'E' is less than the potential 'V', the wave function is made of exponential hyperbolic functions.
- Greater energy = lower energy-potential gap = smaller alpha-value = slower decay
The lower the energy is (the bigger the energy-potential gap is) the faster the function exponentially decays. This makes intuitive sense because we logically didn’t even assume that the particle could even exist in this region. Obviously, the higher the activation energy (the gap) is, the harder it would be for the particle to somehow reach this position.
This is also coherent with our mathematical finding from the infinite square well. The infinite square well is just the finite square well with a HUGE energy-potential gap. We found that in this specific limit, the particle mathematically disappears. We approximately see this in the finite potential well as the wave function goes to zero exponentially fast as the potential goes to infinity (the function exponentially decays so fast that it barely even penetrates the potential barrier at all).
BUT WAIT: some of the people following along may be starting to connect some of the dots as to why this result is so troubling. Psi(x) is the time independent form of the wave function. The wave function squared relates to the probability of finding a particle in a given space. If there exists some wave function in a classically forbidden region, then so does there exist some probability of a particle occupying a space it never should. There is a probability of you falling through the floor, your goldfish swimming out of its tank, and your hat falling through your head. And this probability is quantifiable and experimentally proven to exist.
Takeaway from bound states:
The fact that a particle can be in a place where it does not have enough energy to occupy is VERY significant and shocking. One can see this in a quick example: a ball is thrown against. When thrown, the ball has enough energy to travel through the air. If supplied even more energy, greater than the wall's potential barrier, the ball can travel through the wall (we will call that scattering, but more on that later). In contrast, if the ball does not have enough energy, we would not expect it to go through the wall and rather stop at the wall or bounce back. However, we just proved that according to quantum mechanics there is a possibility, even without enough energy, for the ball to enter the wall’s space (and no we are not talking about deforming the wall; actually, enter the wall). Let me quickly note that real numerical examples show this to be very unlikely, but it is possible. In fact, physicists have used this principle to push reactions forwards without (though usually close to) the necessary energy. We call this potential barrier penetration ‘quantum tunneling.’
|
|
|