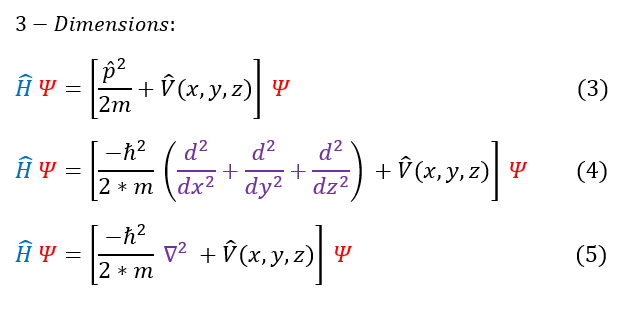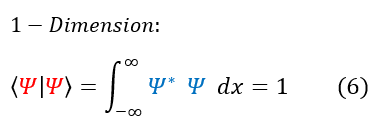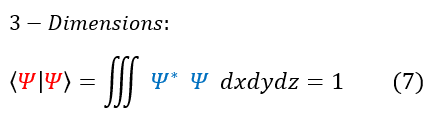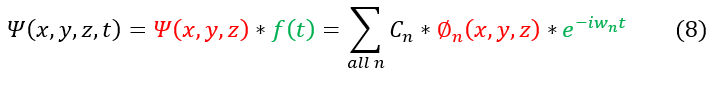|
|
|
So far we have solved a lot of quantum mechanical problems in one dimensions (specifically the x dimension); however, as one may have guessed, particles can exist in 3 dimensions (and theoretically more). As we add in more dimensions, it is important to realize that the x dimension had nothing special about it. Mathematics along the x direction is the same as mathematics along the y and z dimensions.
Let us now look at a 3-dimension Schrödinger equation. The energy operator used to find the Schrödinger equation had zero dependence on us only being in the x direction. We are still just saying: total energy = kinetic energy + potential energy.When we previously said 'p_x' and 'V(x)' we were talking about the total momentum 'p' and the total potential energy 'V,' it just so happened that that was only in the x direction. We can now add on the other directions as so:
Let us now look at a 3-dimension Schrödinger equation. The energy operator used to find the Schrödinger equation had zero dependence on us only being in the x direction. We are still just saying: total energy = kinetic energy + potential energy.When we previously said 'p_x' and 'V(x)' we were talking about the total momentum 'p' and the total potential energy 'V,' it just so happened that that was only in the x direction. We can now add on the other directions as so:
|
|
The purple upside down triangle is what we call the Laplacian. It has numerous mathematical applications (the gradient for example). For quantum, just know that we are calling it the Laplacian and it equals the sum of the second derivatives in a Cartesian coordinate system.
Another difference between 1 dimensional and 3 dimensional quantum mechanics is the normalization. Again, we can go back to our mathematical roots and remember that in order for the wave function squared to be a probability density, it must have an area of 1. This is still true for a probability density in three dimensions, we just have more space to sum over. We can now modify the normalization as so:
Another difference between 1 dimensional and 3 dimensional quantum mechanics is the normalization. Again, we can go back to our mathematical roots and remember that in order for the wave function squared to be a probability density, it must have an area of 1. This is still true for a probability density in three dimensions, we just have more space to sum over. We can now modify the normalization as so:
|
|
As one might notice above, just like in one dimension, we are still using the standing wave approximation for the Schrödinger equation in 3D (that we can separate out time and position). Time does not change as we go from 1 dimension to 3 dimensions; hence, our full time dependent solution will still take the form:
|
|
|