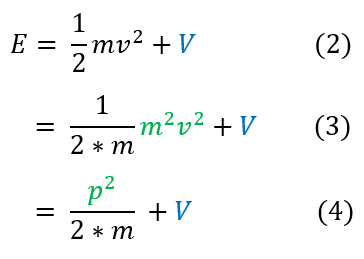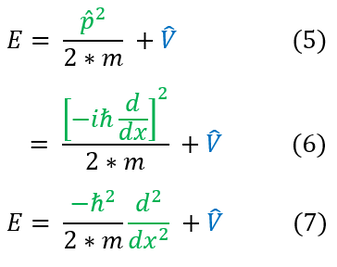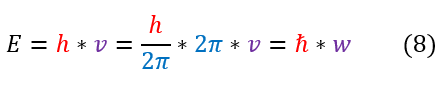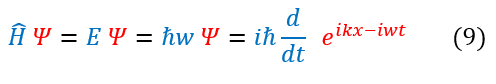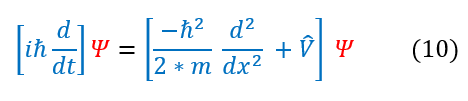Mind Network - Samuel Solomon
The Schrödinger Equation
The "Derivation"
It is time for the most wonderful part of quantum: the Schrödinger equation. This sole equation is not only the basis of complex quantum mechanics, but it is also the hardest equation to solve for a multinuclear system (but we will get there through some approximations later).
The total energy of a system is broken up into two part: kinetic and potential energy (we will ignore rotational energy for now, but perturbations of it will be added to the potential energy term later). Let us break down the total energy below:
In order to make sure everyone is following, let us review some key steps below:
2: Total energy can be broken up into a kinetic and potential portion
2 to 3: Multiple by m/m
3 to 4: Mass * Velocity = Momentum
4 to 5: Switch between the eigenvalues (observables) to their corresponding operators
5 to 6: Return the eigenvalue for the momentum operator
6 to 7: Simplify the expression
Let us recall the black body radiation problem that led to quantum mechanics. In the problem, Planck realized / regretfully noticed that energy is not a continuous spectrum. Rather, energy values can only be multiples of some constant (now called Planck’s constant). It was found that the observable (eigenvalue) for the total energy was:
2: Total energy can be broken up into a kinetic and potential portion
2 to 3: Multiple by m/m
3 to 4: Mass * Velocity = Momentum
4 to 5: Switch between the eigenvalues (observables) to their corresponding operators
5 to 6: Return the eigenvalue for the momentum operator
6 to 7: Simplify the expression
Let us recall the black body radiation problem that led to quantum mechanics. In the problem, Planck realized / regretfully noticed that energy is not a continuous spectrum. Rather, energy values can only be multiples of some constant (now called Planck’s constant). It was found that the observable (eigenvalue) for the total energy was:
For a general wave function we can think about a single operator to yield this total energy value:
An operator cannot be proven to be true as it has no true meaning, but one can see that this ansatz (educated guess) does produce the correct observable (eigenvalue). We can now combine these two definitions for the full energy into the expanded Schrödinger equation below:
Note: we cannot just cross out the psi term on either side. This is because the operators on both sides of the equations rely on there being a psi after it. An operator needs a wave function to act on to have physical meaning. If this is confusing, think about this: if there is no psi, what does d/dt mean? The change in nothing over the change in time? Only with the psi on both sides are they equal.
Note: the left hand side (LHS) has an imaginary term, while the right hand side (RHS) does not. This means that no matter which psi we use, the time dependent term needs an imaginary component.
Let us also appreciate that what I wrote above is not a proof of the Schrödinger equation!! Let us consider a few reasons why:
1. E = h_bar*omega. This was a postulate to make sense of the black body radiation problem. It is experimentally
verified for a free particle, but not rigorously proven mathematically (we keep adding decimal places to the
constant). We will use this operator to find energies of states other than free particles (generalize).
2. The E = h_bar*omega is the total energy (not only kinetic or potential).
3. The whole concept of operators is based on postulates. Can we revert any eigenvalue to its operator form?
4. Those familiar with waves will know that omega (w) follows a dispersion relation
While not a proof, through an understanding of our postulates, we can use this equation in ways to extrapolate information from the physical world (information we would not have intuitively assumed before quantum).
Note: the left hand side (LHS) has an imaginary term, while the right hand side (RHS) does not. This means that no matter which psi we use, the time dependent term needs an imaginary component.
Let us also appreciate that what I wrote above is not a proof of the Schrödinger equation!! Let us consider a few reasons why:
1. E = h_bar*omega. This was a postulate to make sense of the black body radiation problem. It is experimentally
verified for a free particle, but not rigorously proven mathematically (we keep adding decimal places to the
constant). We will use this operator to find energies of states other than free particles (generalize).
2. The E = h_bar*omega is the total energy (not only kinetic or potential).
3. The whole concept of operators is based on postulates. Can we revert any eigenvalue to its operator form?
4. Those familiar with waves will know that omega (w) follows a dispersion relation
While not a proof, through an understanding of our postulates, we can use this equation in ways to extrapolate information from the physical world (information we would not have intuitively assumed before quantum).
|
|
|