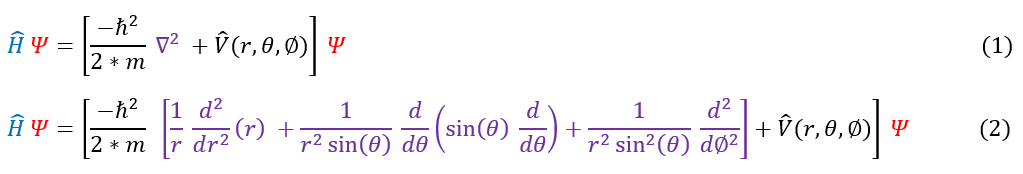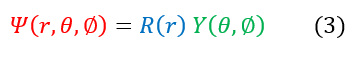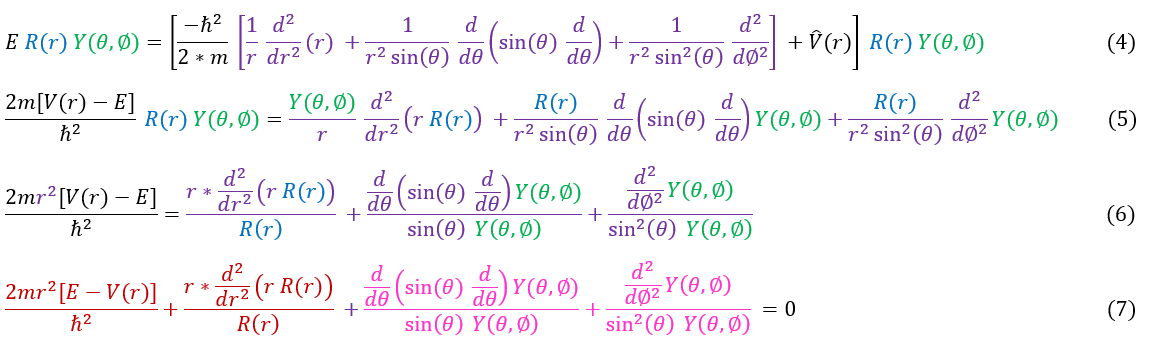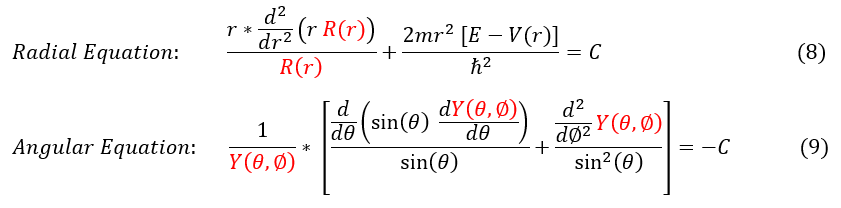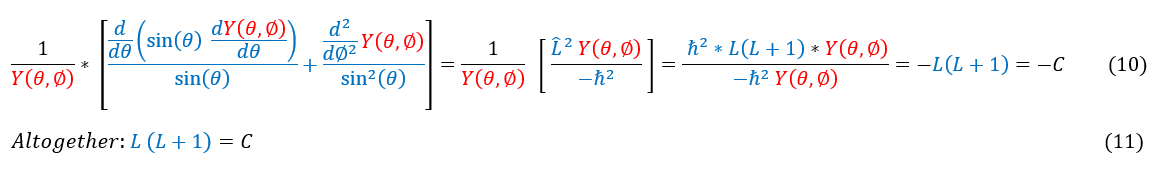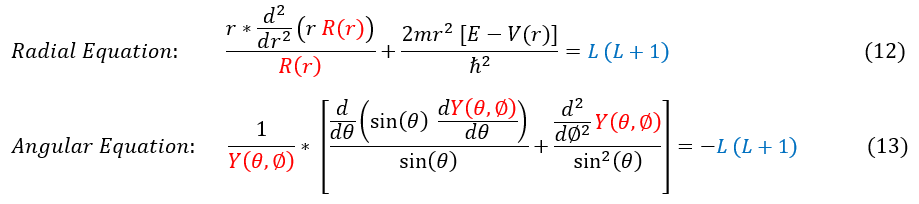Mind Network - Samuel Solomon
Schrödinger Equation
Spherical Symmetric Potential
|
|
|
It is best to begin our discussion of solving quantum mechanical problems in spherical coordinates with (one of) the easiest potentials out there: spherically symmetric potentials. Spherically symmetric potentials are potentials that have no angular variations: V(r, theta, phi) => V(r).
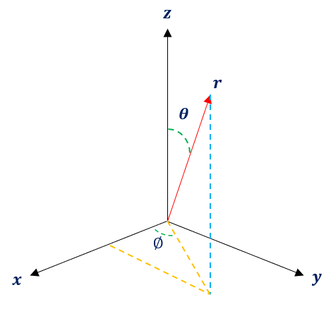
Before we begin our analysis, let us quickly remind ourselves of our spherical coordinates definition (some books vary). We define our spherical coordinates as follows:
Before we begin our analysis, let us quickly remind ourselves of our spherical coordinates definition (some books vary). We define our spherical coordinates as follows:
It is important to note that even among scientists, people tend to define these coordinates differently. But as long as we are internally consistent, it is okay. To be clear, my coordinates are defined as follows:
Theta: The angle the point makes with the z axis
Phi: The angle the point makes with the x-axis in the x-y plane
r: the distance between the point and the origin (Some call it 'Rho')
We are now ready to work with our Schrödinger equation (in spherical coordinates) below (see Schrödinger Equation (Spherical Coordinates) page for a recap):
Theta: The angle the point makes with the z axis
Phi: The angle the point makes with the x-axis in the x-y plane
r: the distance between the point and the origin (Some call it 'Rho')
We are now ready to work with our Schrödinger equation (in spherical coordinates) below (see Schrödinger Equation (Spherical Coordinates) page for a recap):
Altogether, this equation looks daunting, but we can still apply our standing wave approximation to the spherical form of the Schrödinger equation. Since we are working with a spherically symmetric potential, we will only separate out the radial solution from the angular component. We can write our ansatz out explicitly below:
Please note that I am using the notation 'R(r)' and 'Y(theta, phi)' for the radial and angular solution respectively. This is just to match the most common notation used for spherically symmetric potentials online.
We can now plug in our ansatz back into the Schrödinger equation:
We can now plug in our ansatz back into the Schrödinger equation:
In order to make sure everyone is following, let us review some key steps below:
4: Schrödinger equation with the spherical Laplacian (purple), spherically symmetric potential, and ansatz (equation 3)
4 to 5: Move V(r) and the constant in front of the Laplacian to the LHS. Distribute 'R' and 'Y' throughout the Laplacian
5 to 6: Multiply both sides by 'r^2' and divide both sides by 'R(r) * Y(theta, phi)'
6 to 7: Bring the black term with the 'V(r) - E' to the RHS, so that the equation equals zero (a constant)
We can immediately notice in equation 7 that the dark red terms only depends on the variable 'r' and the pink terms only depend on the angular components 'theta' and 'phi.' This means that if I move the radius of the particle, but not the angle, the whole dark red term CANNOT change (it is a constant). If I move the angle of the particle, but not the radius, the whole pink term CANNOT change (the dark red term will not change and zero is just a constant). Hence, both the pink and the red term are CONSTANTS. To solve any spherically symmetric potential, all you have to do is solve the dark red term (the radial component) and the pink term (the angular component). We can explicitly right this below:
4: Schrödinger equation with the spherical Laplacian (purple), spherically symmetric potential, and ansatz (equation 3)
4 to 5: Move V(r) and the constant in front of the Laplacian to the LHS. Distribute 'R' and 'Y' throughout the Laplacian
5 to 6: Multiply both sides by 'r^2' and divide both sides by 'R(r) * Y(theta, phi)'
6 to 7: Bring the black term with the 'V(r) - E' to the RHS, so that the equation equals zero (a constant)
We can immediately notice in equation 7 that the dark red terms only depends on the variable 'r' and the pink terms only depend on the angular components 'theta' and 'phi.' This means that if I move the radius of the particle, but not the angle, the whole dark red term CANNOT change (it is a constant). If I move the angle of the particle, but not the radius, the whole pink term CANNOT change (the dark red term will not change and zero is just a constant). Hence, both the pink and the red term are CONSTANTS. To solve any spherically symmetric potential, all you have to do is solve the dark red term (the radial component) and the pink term (the angular component). We can explicitly right this below:
Equation 9 may look a bit familiar. In fact, it has a hidden L^2 operator inside. We can pull it out below:
This leads us to our full radial and angular equations below:
|
|
|