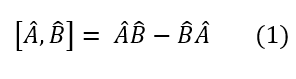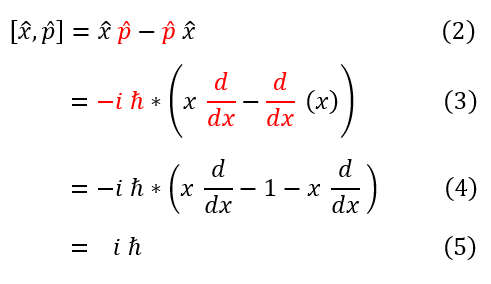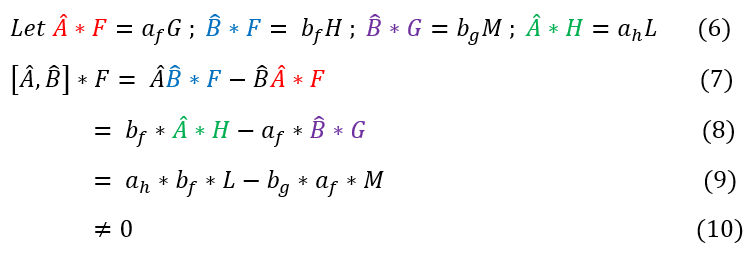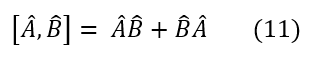Mind Network - Samuel Solomon
Commutation
Commutators between quantum operators will be a big part in determining quantum properties such as uncertainty (more on that soon). Let us introduce the definition and example of the concept:
No, this is not zero. If one has a good background in matrix multiplication, then this may be obvious. If not, an easy way to see this intuitively is with the derivative operator, as was the case for the momentum operator. As an example, let us commute x and p:
In order to make sure everyone is following, let us review below:
2: The definition of the commutator
2 to 3: Plugging in the momentum operator we found above. -i*h_bar was factored out.
3 to 4: Operators act on functions, so p*x is p*x on a function. We therefore need the chain rule to evaluate d/dx(x)
4 to 5: Simplify the expression
While this result was used as an example of commutators, its significance will be shown later on (with respect to uncertainties). For now, just know that if 2 operators commute, then p*x = x*p (which is a useful way to switch two operators around.
One may start to wonder what is the significance of operators commuting? To answer this, one must remember that operators do not have significance outside of the function they operate on. When we say AB - BA = 0, we are really saying that 'AB - BA' on a function is zero. It takes some thought, but this only works if A and B both do not change the function (only scale the function). This means that operators A and B only commute if their exists a shared eigenfunction for both operator A and B (they do not need to share all of them, but at least one).
To proof this, let us do a proof by contradiction. Let us consider what would happen if they were not eigenfunctions of the same operator to see why this is true (note: this is not the most rigorous proof as we could have different variations of the same problem; however, all will come out to the same answer that [ A , B ] does not equal 0 if they do not share any eigenfunction. It is a fun exercise to complete if you have time):
2: The definition of the commutator
2 to 3: Plugging in the momentum operator we found above. -i*h_bar was factored out.
3 to 4: Operators act on functions, so p*x is p*x on a function. We therefore need the chain rule to evaluate d/dx(x)
4 to 5: Simplify the expression
While this result was used as an example of commutators, its significance will be shown later on (with respect to uncertainties). For now, just know that if 2 operators commute, then p*x = x*p (which is a useful way to switch two operators around.
One may start to wonder what is the significance of operators commuting? To answer this, one must remember that operators do not have significance outside of the function they operate on. When we say AB - BA = 0, we are really saying that 'AB - BA' on a function is zero. It takes some thought, but this only works if A and B both do not change the function (only scale the function). This means that operators A and B only commute if their exists a shared eigenfunction for both operator A and B (they do not need to share all of them, but at least one).
To proof this, let us do a proof by contradiction. Let us consider what would happen if they were not eigenfunctions of the same operator to see why this is true (note: this is not the most rigorous proof as we could have different variations of the same problem; however, all will come out to the same answer that [ A , B ] does not equal 0 if they do not share any eigenfunction. It is a fun exercise to complete if you have time):
In order to make sure everyone is following, let us review below:
6: This will be our starting position. A and B are not eigenfunctions, and hence do not scale the function (but change it)
7: This is the definition of the commutator, but applied to a function.
7 to 8: Using equation 6, replace the highlighted operators
8 to 9: Using equation 6, replace the highlighted operators
9 to 10: L and M are different functions (not the same by any scalar). Therefore, no matter the scalar, it is non-zero
We need them both share an eigenfunction in order to end up with the same function in the end. Only then can the scalars cancel to zero and it commute. We call these eigenfunctions 'mutual eigenfunctions' or 'simultaneous eigenfunctions.'
The last note about commutators is the anti-commutator. It has less significance, but there are important operators that do anti-commute. The definition is below:
6: This will be our starting position. A and B are not eigenfunctions, and hence do not scale the function (but change it)
7: This is the definition of the commutator, but applied to a function.
7 to 8: Using equation 6, replace the highlighted operators
8 to 9: Using equation 6, replace the highlighted operators
9 to 10: L and M are different functions (not the same by any scalar). Therefore, no matter the scalar, it is non-zero
We need them both share an eigenfunction in order to end up with the same function in the end. Only then can the scalars cancel to zero and it commute. We call these eigenfunctions 'mutual eigenfunctions' or 'simultaneous eigenfunctions.'
The last note about commutators is the anti-commutator. It has less significance, but there are important operators that do anti-commute. The definition is below:
|
|
|