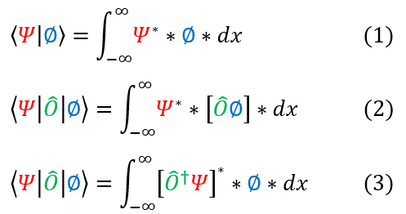Mind Network - Samuel Solomon
Dirac Notation
Let us now move onto the most common notation for using quantum operators called Dirac Notation (though some may see the resemblance to an inner product). Let me quickly highlight the word notation. Quantum math can be very very (very) messy. So let us just start to introduce this nice notation here:
In order to make sure everyone is following, let us review:
9: The left hand side is called Dirac notation and is always equivalent to the right hand side
10: The operator is normally placed in the middle of the bracket, and acts on the function to the right.
11: If the operator acts on the function to the left, it is called the "adjoint" operator (many just say "dagger")
Expressions 10 and 11 are equivalent expressions; hence, many times the adjoint operator and the operator have different functional representation (in order to make sure that the ending expression is the same). Do note that I am assuming that both psi and phi are in the same basis set (like e^ikx).
Like any mathematical approach to working in multiple dimensions, matrices are a very helpful tool. Some of you may recall the term adjoint in some linear algebra class. It is in fact the same adjoint. If you were in matrix format, you would take the adjoint of the matrix to solve for the "dagger" form of the operator.
While <A|B> may appear as one object, it can actually be broken down (and appear in reverse order). In order to familiarize ourselves with these names, I broke the nomenclature down below:
9: The left hand side is called Dirac notation and is always equivalent to the right hand side
10: The operator is normally placed in the middle of the bracket, and acts on the function to the right.
11: If the operator acts on the function to the left, it is called the "adjoint" operator (many just say "dagger")
Expressions 10 and 11 are equivalent expressions; hence, many times the adjoint operator and the operator have different functional representation (in order to make sure that the ending expression is the same). Do note that I am assuming that both psi and phi are in the same basis set (like e^ikx).
Like any mathematical approach to working in multiple dimensions, matrices are a very helpful tool. Some of you may recall the term adjoint in some linear algebra class. It is in fact the same adjoint. If you were in matrix format, you would take the adjoint of the matrix to solve for the "dagger" form of the operator.
While <A|B> may appear as one object, it can actually be broken down (and appear in reverse order). In order to familiarize ourselves with these names, I broke the nomenclature down below:
|
|
|