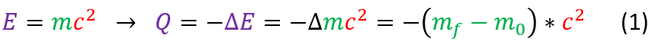Mind Network - Samuel Solomon
Introduction to Fusion
Applications and Challenges
It is time to bring up the celebrity of this course: Nuclear Fusion. However, before blindly diving deep into the mathematics of fusion, I think it is important to motivate why people care so much about it. Additionally, talk about the challenges that the field still faces.
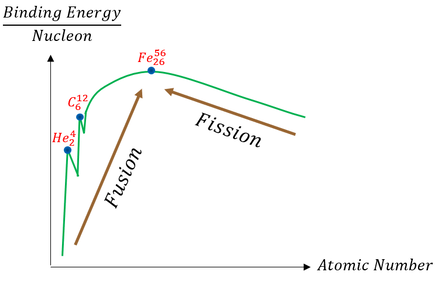
First let us define fusion. Fusion is the process of combining two nuclei to create a more stable product. In the process, the excess energy is released and converted into electricity. To begin the discussion of fusion, let us recall the nuclear binding energy diagram showing the stability of all the nuclei relative to each other:
First let us define fusion. Fusion is the process of combining two nuclei to create a more stable product. In the process, the excess energy is released and converted into electricity. To begin the discussion of fusion, let us recall the nuclear binding energy diagram showing the stability of all the nuclei relative to each other:
As one can hopefully tell from the diagram above, Fe-56 is the most stable nuclei. Fusing two lighter nuclei together therefore has the potential of creating a more stable system (allowing for the release/ capture of excess energy). Compared to fission, which on average releases around 0.9 Mev, fission can release around 7 Mev (see the bigger slope on the graph).
Just like in the case for fission (see first page), this energy comes from the mass, with total amount of nucleons conserved overall. We can therefore use Einstein's famous equation again to find the energy released: the Q-value of the reaction:
Just like in the case for fission (see first page), this energy comes from the mass, with total amount of nucleons conserved overall. We can therefore use Einstein's famous equation again to find the energy released: the Q-value of the reaction:
And that summarizes fusion. As long as the mass-energy conversion (Q-value, energy released) is greater than the energy you supplied to fuse the system, there is a net gain/ production of energy. The benefits of fusion over other sources are:
* The fuel for fusion is abundant and has a high energy density: don't need to go mining/ fracking for materials
* There is no green house gas emission: no CO2, SO2, NO2, CFCs, CH4 ... etc released
* No long lived waste products formed: everything can be disposed on in <100 years
* Safer (relatively) due to no chain reactions and need to continuously feed in fuel to proceed: easy to stop, hard to run
* minimum land/ water needed: no seasonal variations when running the reactor
The material is so abundant (for example, you can find Li, one of the atoms needed, directly in the ocean), that people predict we would have an energy source for thousands of years. On top of all of these amazing benefits over other carbon-based fuels and dangerous fission reactors, fusion also has other cool applications outside of clean energy, such as:
* Create planetary-like magnetic fields: see levitated dipole experiment (MIT)
* Space propulsion: using fusion rockets
* Nuclear weapons: less exciting, but still worth mentioning.
And, honestly, who knows what else fusion could be used for. I say this because there is one major drawback to fusion energy right now: IT DOESN'T WORK!
Now that ones been officially excited about fusion energy, it is time to start discussing its flaws (and yes, one big one is that its not possible yet). The simplest reason fusion doesn't work yet can be depicted below:
* The fuel for fusion is abundant and has a high energy density: don't need to go mining/ fracking for materials
* There is no green house gas emission: no CO2, SO2, NO2, CFCs, CH4 ... etc released
* No long lived waste products formed: everything can be disposed on in <100 years
* Safer (relatively) due to no chain reactions and need to continuously feed in fuel to proceed: easy to stop, hard to run
* minimum land/ water needed: no seasonal variations when running the reactor
The material is so abundant (for example, you can find Li, one of the atoms needed, directly in the ocean), that people predict we would have an energy source for thousands of years. On top of all of these amazing benefits over other carbon-based fuels and dangerous fission reactors, fusion also has other cool applications outside of clean energy, such as:
* Create planetary-like magnetic fields: see levitated dipole experiment (MIT)
* Space propulsion: using fusion rockets
* Nuclear weapons: less exciting, but still worth mentioning.
And, honestly, who knows what else fusion could be used for. I say this because there is one major drawback to fusion energy right now: IT DOESN'T WORK!
Now that ones been officially excited about fusion energy, it is time to start discussing its flaws (and yes, one big one is that its not possible yet). The simplest reason fusion doesn't work yet can be depicted below:
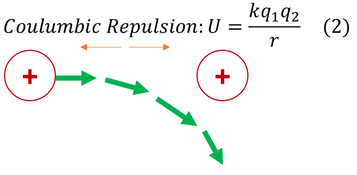
Unfortunately for fusion, the fact of the matter is that two nuclei (both positively charged) do NOT want to get close enough to fuse. Remember in fission, a neutral neutron was shot at the nucleus, and the nucleus broke apart. Bringing nuclei together provides a whole new set of coulomb challenges. As the positive nucleus approaches, it is MUCH more likely to diverge away (through a process known as coulomb scattering: depicted above).
Regardless of the troubles, scientists have continued to pursue this research using a wide variety of different fusion systems/ techniques (we won't go through them all). To compare different fusion systems, scientists generally use a value known as Q, which is a ratio of the output energy to the input energy (this is NOT the same as the Q-value depicting the energy released, though the naming could be better):
Regardless of the troubles, scientists have continued to pursue this research using a wide variety of different fusion systems/ techniques (we won't go through them all). To compare different fusion systems, scientists generally use a value known as Q, which is a ratio of the output energy to the input energy (this is NOT the same as the Q-value depicting the energy released, though the naming could be better):
We can interpret the Q-value as follows:
* Q > 1: We produced a net gain of energy. Fusion works, and can provide a new clean energy source.
* Q = 1: We are net nuetral. Cannot provide any energy to public.
* Q < 1: We are using more energy to run the reaction than we can get out. Fusion is a failure.
We are not experimentally at a Q-value > 1 yet, but there are theoretical fusion systems out there such as SPARC and ITER being built/ tested now. Currently, the best known design to get a high Q-value is known as the Tokamak (which we will focus on throughout this course).
* Q > 1: We produced a net gain of energy. Fusion works, and can provide a new clean energy source.
* Q = 1: We are net nuetral. Cannot provide any energy to public.
* Q < 1: We are using more energy to run the reaction than we can get out. Fusion is a failure.
We are not experimentally at a Q-value > 1 yet, but there are theoretical fusion systems out there such as SPARC and ITER being built/ tested now. Currently, the best known design to get a high Q-value is known as the Tokamak (which we will focus on throughout this course).
|
|
|