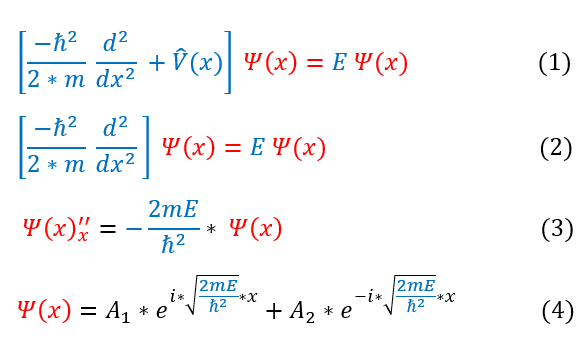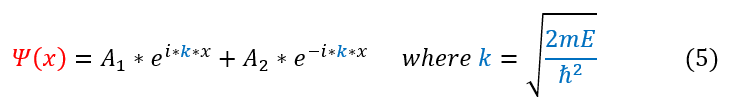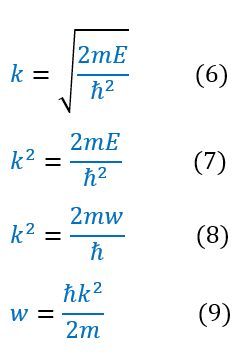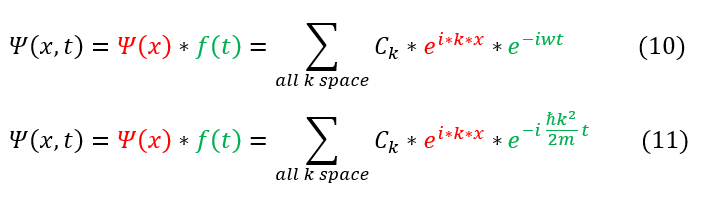To solve the Schrödinger equation, we need to define a potential. The most simply potential possible to define is V(x) = 0. Physically, this means that the particle has no interactions with any other particle (sits inside a vacuum). The position dependent (time independent) Schrödinger equation reduces to:
In order to make sure everyone is following, let us review some key steps below:
1: The time independent Schrödinger equation
1 to 2: Set V(x)=0 for a free particle
2 to 3: Move all constants on the right side
3 to 4: Solve the differential equation
We can recognize equation 4 as a plane wave (e^ikx) with a k value the square root term. We can now make this replacement below:
1: The time independent Schrödinger equation
1 to 2: Set V(x)=0 for a free particle
2 to 3: Move all constants on the right side
3 to 4: Solve the differential equation
We can recognize equation 4 as a plane wave (e^ikx) with a k value the square root term. We can now make this replacement below:
While we previously found energy to be constant, we have not defined what the constant is. We additionally found (in the black body radiation experiment) that the total energy for a free particle (only a free particle) is h_bar*w. h_bar is a constant, but w depends on the wave (see dispersion relations. Not discussed in this course, but an integral part of wave mechanics). We can find our relation below:
In order to make sure everyone is following, let us review some key steps below:
7: Out k constant we found in equation 5
7 to 8: Square both sides
8 to 9: Replace E with h_bar*w
9 to 10: Solve for w in terms of k.
We can now time evolve the Schrödinger equation by adding in the time evolution equation we previously solved for. I will sum over all k space (for all the constants k can be) as those represent all possible basis states for the free particle. The solution had e^ikx and e^-ikx, but I can absorb the negative sign into a different k value. This yields the full wave function as:
7: Out k constant we found in equation 5
7 to 8: Square both sides
8 to 9: Replace E with h_bar*w
9 to 10: Solve for w in terms of k.
We can now time evolve the Schrödinger equation by adding in the time evolution equation we previously solved for. I will sum over all k space (for all the constants k can be) as those represent all possible basis states for the free particle. The solution had e^ikx and e^-ikx, but I can absorb the negative sign into a different k value. This yields the full wave function as:
|
|
|
