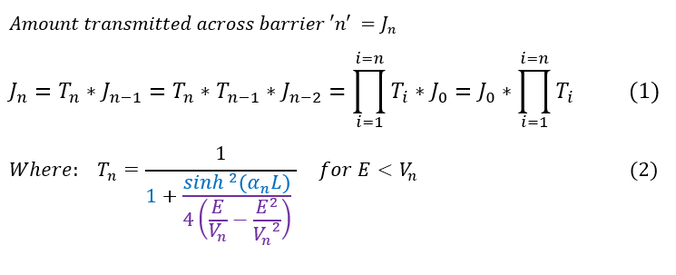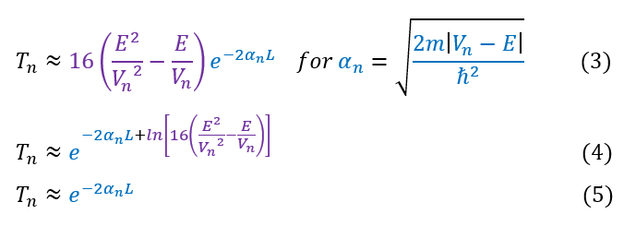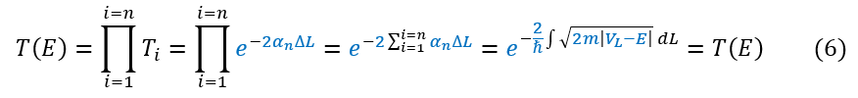Mind Network - Samuel Solomon
Quantum Tunneling
Changing Potential
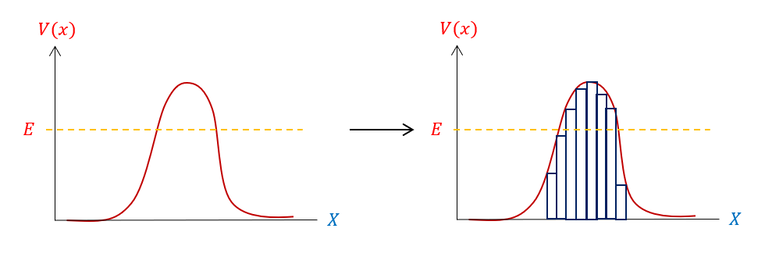
So far, all of our potential barriers have been constant step functions. One might have questions the usefulness of such a simple example: most potentials are not constant in space after all. To illuminate why we built up such a strong base in these basic examples, let us consider our first changing potential:
As illuminated in the picture, the basic plan to tackle changing potential barriers is to, in fact, approximate them as small thin constant potential barrier (exactly the same type of problem we saw on the last page). We still have a wave starting from the left and hitting a small barrier (with some reflection and some transmission), except now as it exits the first barrier, it again immediately hits another barrier (of a different potential). It proceeds like this all the way through the potential. One might recognize that the premise is in fact analogous to how we solve for an area under a curve using integration.
The total amount of the wave being transmitted will be the amount transmitted through the first barrier that is also transmitted through the second and third and fourth and .... all the way through the end. Hence, the total transmission coefficient will be the multiplication of all the transmission fractions from each barrier * the incident wave:
The total amount of the wave being transmitted will be the amount transmitted through the first barrier that is also transmitted through the second and third and fourth and .... all the way through the end. Hence, the total transmission coefficient will be the multiplication of all the transmission fractions from each barrier * the incident wave:
And that is really it! We solved a more complicated problem. We know can do quantum tunneling for any potential V(x) and E(x). Granted, the math may not be too pretty, but that's where Mathematica or Matlab comes in so ...
Just to make sure we are on the same page / understanding though, let us solve a simple, general, changing potential problem. To simplify the math, let us assume that the potential 'V' is always MUCH BIGGER than the energy 'E' of the particle. This means that 'alpha*L' is a huge number and we can make the approximation:
Just to make sure we are on the same page / understanding though, let us solve a simple, general, changing potential problem. To simplify the math, let us assume that the potential 'V' is always MUCH BIGGER than the energy 'E' of the particle. This means that 'alpha*L' is a huge number and we can make the approximation:
We need to solve for the amount of the wave function going out of the total potential barrier (which we will represent as the total transmission coefficient). According to equation 1, the amount of the wave function leaving a given barrier, represented as the probability current 'J_n', is a function of the initial probability current (which is always given based on the initial wave) and the multiplication sum of the transmission coefficients. So the only unknown here is the multiplication sum of the transmission coefficients, which we can solve for below:
In order to make sure everyone is following, let us review some key steps below:
The 'pi-shaped' symbol is a multiplication sum that equals T_1 * T_2 * ... * T_n
When we multiply e^x functions together it is the same as adding up all their exponents: e^ix * e^iy = e^(ix+iy)
In the limit of small deltaL widths, the infinitesimal summation is just an integral
And now, with a V(x) potential function, you can easily solve the integral (with some bounds) to find the total transmission coefficent for the wave exiting the potential.
The 'pi-shaped' symbol is a multiplication sum that equals T_1 * T_2 * ... * T_n
When we multiply e^x functions together it is the same as adding up all their exponents: e^ix * e^iy = e^(ix+iy)
In the limit of small deltaL widths, the infinitesimal summation is just an integral
And now, with a V(x) potential function, you can easily solve the integral (with some bounds) to find the total transmission coefficent for the wave exiting the potential.
|
|
|