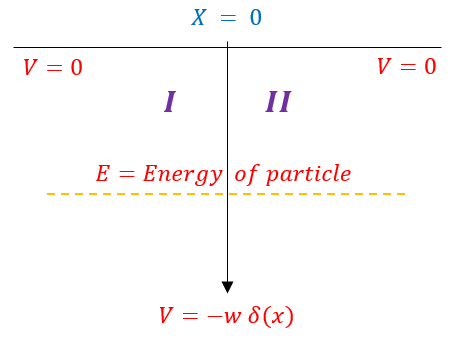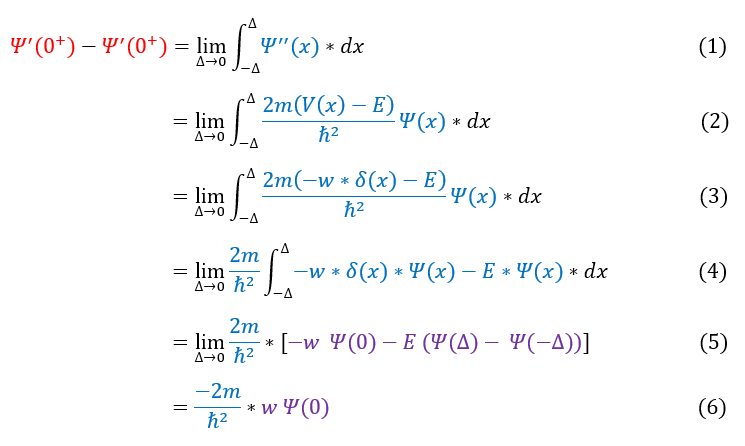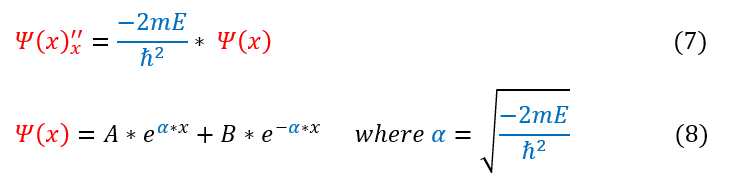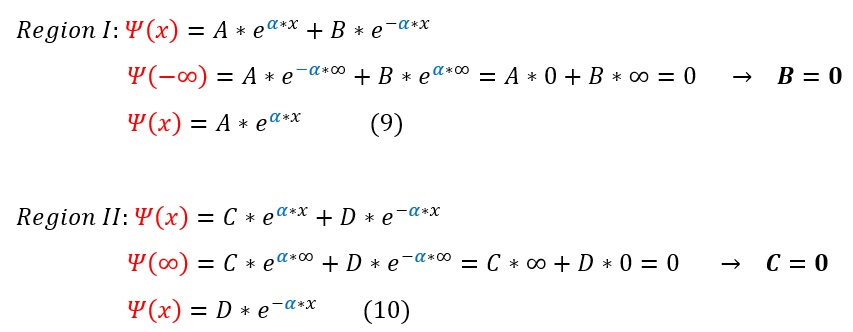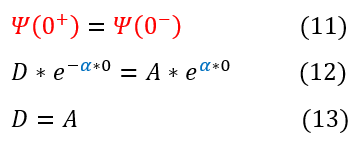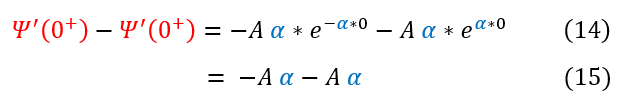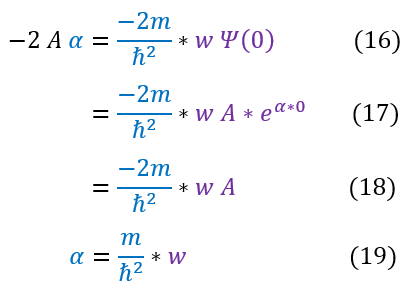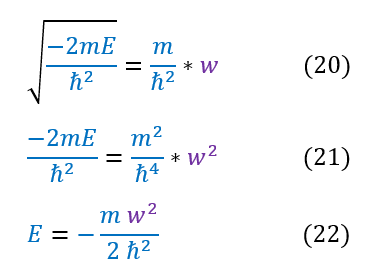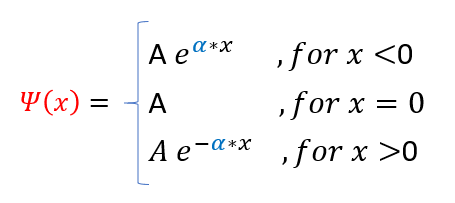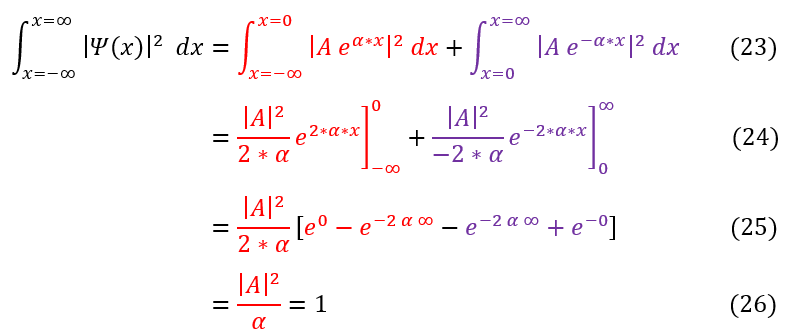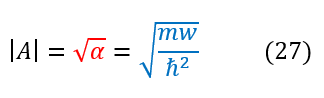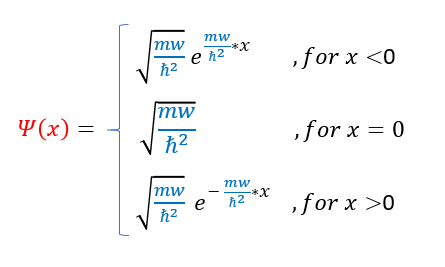Mind Network - Samuel Solomon
Delta Function Potential Well
A Delta function potential well is a potential where a particle experiences a potential of zero everywhere exept one place (where it experiences a potential of infinity). Hence, the particle physically experiences no outside forces (is a free particle) everywhere but one place. A real life example of this potential would be an electron flowing between two metal surfaces. Inside a given metal, the electron can essentially flow freely (like a free particle, V(x) = 0); however, at the surface of the metal there is a small gap. This space, the electron cannot flow freely and experiences a HUGE barrier (very big, like infinity).
One can also have a double Delta function potential well. This approximately models a hydrogen molecule in free space. The electron cannot access the nucleus (hence a huge potential, essentially infinity, at 2 specific locations). Meanwhile, everywhere else the electron does not experience such a huge effect (obviously it still feels the nucleus, but the force decays exponentially with distance).
Let us now solve a real example of a single Delta function potential. We can model the potential well below:
One can also have a double Delta function potential well. This approximately models a hydrogen molecule in free space. The electron cannot access the nucleus (hence a huge potential, essentially infinity, at 2 specific locations). Meanwhile, everywhere else the electron does not experience such a huge effect (obviously it still feels the nucleus, but the force decays exponentially with distance).
Let us now solve a real example of a single Delta function potential. We can model the potential well below:
To tackle this problem, let us divide the graph into 2 different sections. We will take energy to be some number less than zero, but greater than the Delta function potential (bound in the middle of the potential function). We will label the first section to be on the left and the second section to be on the right.
We can easily solve for the wave function in a given section, but in order to connect the solutions we must understand how they meet up. In order to sketch this, we must know know two properties of the wave function at a boundary:
1. No matter the potential, the wave function must be continuous
2. The slope of the wave function is only continuous for a finite potential barrier
Unfortunately, a Delta function is an infinite barrier at a point (a Delta function is a rectangle with area one with the width of the rectangle squeezed to zero). Therefore, in order to solve this problem, we need to know the jump discontinuity for the slope. We generally call this the jump condition. We can mathematically find this below:
We can easily solve for the wave function in a given section, but in order to connect the solutions we must understand how they meet up. In order to sketch this, we must know know two properties of the wave function at a boundary:
1. No matter the potential, the wave function must be continuous
2. The slope of the wave function is only continuous for a finite potential barrier
Unfortunately, a Delta function is an infinite barrier at a point (a Delta function is a rectangle with area one with the width of the rectangle squeezed to zero). Therefore, in order to solve this problem, we need to know the jump discontinuity for the slope. We generally call this the jump condition. We can mathematically find this below:
In order to make sure everyone is following, let us review some key steps below:
1: The mathematical check to see if the slope changes at the boundary (see the last page for details)
1 to 2: Plug in the time independent Schrödinger equation
2 to 3: Plug in the Delta function potential specific to this problem
3 to 4: Pull out the constants from the integral
4 to 5: Solve the integral (Note: the delta function is zero in every place except when x = 0)
5 to 6: Evaluate the limit to simplify
Now that we know how to patch the two solutions together, let us evaluate the solution in both regions. They both are classically forbidden regions, and hence follow the same general form:
1: The mathematical check to see if the slope changes at the boundary (see the last page for details)
1 to 2: Plug in the time independent Schrödinger equation
2 to 3: Plug in the Delta function potential specific to this problem
3 to 4: Pull out the constants from the integral
4 to 5: Solve the integral (Note: the delta function is zero in every place except when x = 0)
5 to 6: Evaluate the limit to simplify
Now that we know how to patch the two solutions together, let us evaluate the solution in both regions. They both are classically forbidden regions, and hence follow the same general form:
In order to make sure everyone is following, let us review some key steps below:
7: The time independent Schrödinger equation, where E is a negative number
7 to 8: The solution to the time independent Schrödinger equation
We now add the normalization constraint (decays at +/- infinity) to the wave function:
7: The time independent Schrödinger equation, where E is a negative number
7 to 8: The solution to the time independent Schrödinger equation
We now add the normalization constraint (decays at +/- infinity) to the wave function:
We can now start to patch together these two solutions. The first principle to note is that the wave function must be continuous at the boundary (x = 0):
The second principle to note is that the slope of the wave function for an infinite potential barrier is non-zero. We can apply this to the wave function below:
We also previously solved for the general jump condition equation in equation 6. Setting the two equal to each other yields:
Alpha is a function of energy. Hence, we can now solve for the particle's energy:
In order to make sure everyone is following, let us review some key steps below:
20: We set equation 19 and the alpha value in equation 8 equal to each other
20 to 21: Squared both sides
21 to 22: Solved for the energy
Now that we have the particle's energy and general wave function expressions, it is time to write out the full wave function solution:
20: We set equation 19 and the alpha value in equation 8 equal to each other
20 to 21: Squared both sides
21 to 22: Solved for the energy
Now that we have the particle's energy and general wave function expressions, it is time to write out the full wave function solution:
To solve for the constant 'A' we can normalize the wave function to 1:
In order to make sure everyone is following, let us review some key steps below:
23: The definition of normalization (need to integrate over the whole region)
23 to 24: Take the integral (these are common integrals, but one can plug them into wolfram to check)
24 to 25: Plug in the bounds of each integral
25 to 26: e^-infinity is essentially zero
Therefore, the constant 'A' is therefore:
23: The definition of normalization (need to integrate over the whole region)
23 to 24: Take the integral (these are common integrals, but one can plug them into wolfram to check)
24 to 25: Plug in the bounds of each integral
25 to 26: e^-infinity is essentially zero
Therefore, the constant 'A' is therefore:
This leaves us with the final wave functional form as:
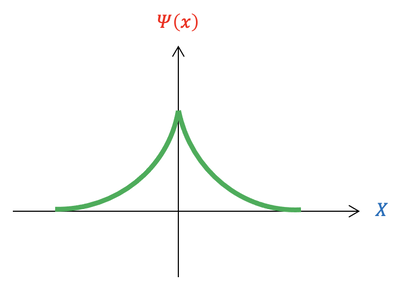
The graph of the wave function is shown below:
|
|
|