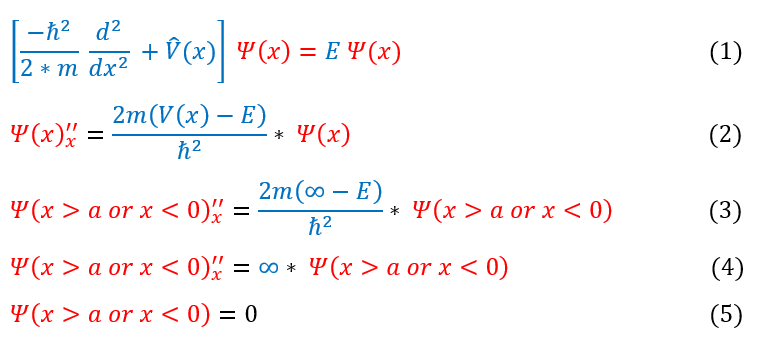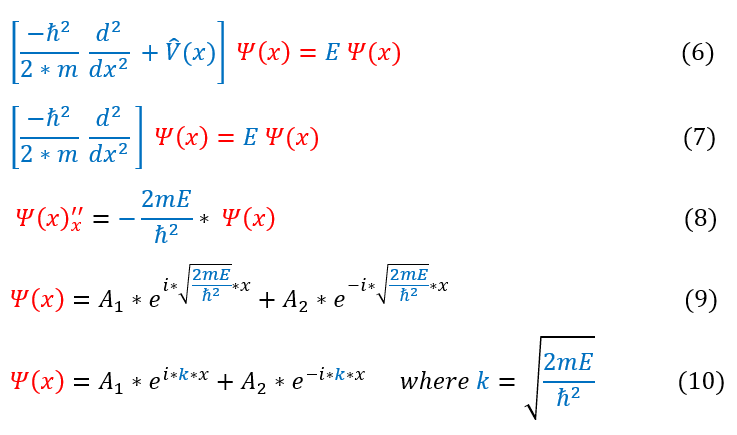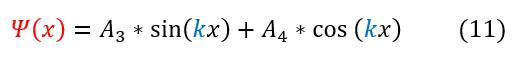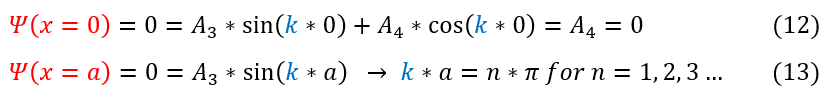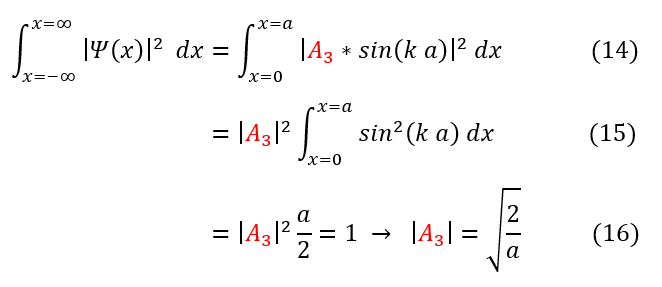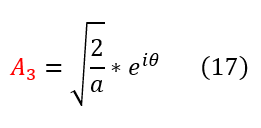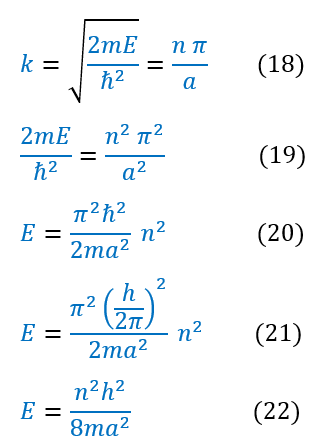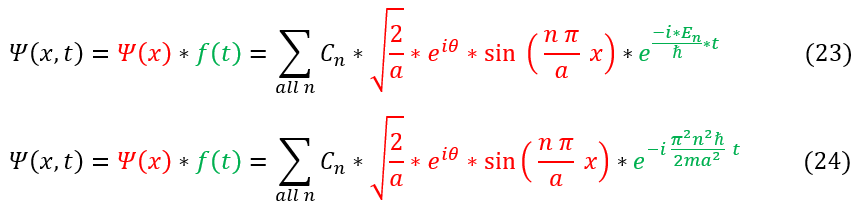Mind Network - Samuel Solomon
Particle in a Box
Infinite Square Well
The Schrödinger equation differentiates particles based on their potential they lie in. For a free particle, previously discussed, we assumed the most basic potential: no potential, V(x)=0. This describes a free particle, but assumes that the particle will never experience a potential at any x-position it occupies. This is unrealistic, and hence we need to start molding our potential to account for this experimental result. In atomic systems, there are places where an electron will NEVER be (or more accurately, it is extremely unlikely). In order to constrain the electron from ever occupying these locations we will set the potential at these location to be infinity (the potential barrier to occupy that location cannot be overcome).
For real applications of this type of problem, we can look at conjugated polymers (series of double bonds or aromatic groups). For these systems, electrons can move (almost) freely inside the band gap (fermi level); however, they cannot escape the molecule (it is not a conductor). The most famous example of these conjugated system (modeled almost exactly by this type of approximation) is the quantum dot: small semiconductors whose color can be changed based on the size of the dot.
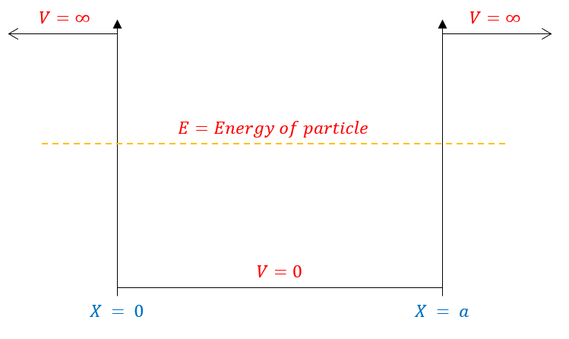
We call this type of problem the "infinite square well" or "particle in a box" and it can be pictorially modeled as:
For real applications of this type of problem, we can look at conjugated polymers (series of double bonds or aromatic groups). For these systems, electrons can move (almost) freely inside the band gap (fermi level); however, they cannot escape the molecule (it is not a conductor). The most famous example of these conjugated system (modeled almost exactly by this type of approximation) is the quantum dot: small semiconductors whose color can be changed based on the size of the dot.
We call this type of problem the "infinite square well" or "particle in a box" and it can be pictorially modeled as:
As one can visually see, the potential is now a piecewise function. We can therefore break up the Schrödinger equation into a part where the potential is infinity and a part where the potential is zero. It is important to note, however, that psi(x) must be a continuous and differentiable function. For now, let us first focus on the part where the potential is infinity:
In order to make sure everyone is following, let us review some key steps below:
1: The time independent Schrödinger equation
1 to 2: Pushing all the constants and V(x) onto one side of the equation
2 to 3: Inserting the potential of infinity, which only describes the wave function for positions outside of the box
3 to 4: 2*infinity and infinity - # is still infinity
4 to 5: This differential equation does not have a clear solution. Only works if the wave function is zero (no particle)
A wave function of zero (no particle) should make sense because this is how we were trying to contain the particle. Let us now refocus our attention to the inside of the box where V(x)=0. We have actually already solved this system before for the free particle and found it to be the plane wave below:
1: The time independent Schrödinger equation
1 to 2: Pushing all the constants and V(x) onto one side of the equation
2 to 3: Inserting the potential of infinity, which only describes the wave function for positions outside of the box
3 to 4: 2*infinity and infinity - # is still infinity
4 to 5: This differential equation does not have a clear solution. Only works if the wave function is zero (no particle)
A wave function of zero (no particle) should make sense because this is how we were trying to contain the particle. Let us now refocus our attention to the inside of the box where V(x)=0. We have actually already solved this system before for the free particle and found it to be the plane wave below:
We can expand the Euler form of e^ikx to get a solution composed of sin and cosines with complex coefficients as so:
While this was the solution to the free particle, we still have to consider the boundary conditions set by the infinite potential. This solution only exists between x=0 to x=a; however the particle must go to zero at x=0 and x=a (because the potential goes to infinity). We therefore have 2 boundary conditions for the infinite square well:
1. psi(x=0) = 0
2. psi(x=a) = 0
We can apply these two boundary conditions below:
1. psi(x=0) = 0
2. psi(x=a) = 0
We can apply these two boundary conditions below:
In order to make sure everyone is following, let us review some key steps below:
12: The wave function has to disappear at x = 0. At x = 0, the wave function equals the constant A_4; hence A_4 = 0
13: The wave function has to disappear at x = a. A_3 cannot also be zero (or else there is no particle; psi(x)=0). The
only way for the equation to always be zero is if the sin term is always zero. This only occurs when k*a is some
integer multiple of pi
Note that if k = 0, then the sin(kx) term is always zero, and hence (just like if A_3 = 0), the whole wave function term is just zero. This would mean that there is no particle present at all (a possibility, but trivial to note).
To find the constant A_3, let us normalize the wave function:
12: The wave function has to disappear at x = 0. At x = 0, the wave function equals the constant A_4; hence A_4 = 0
13: The wave function has to disappear at x = a. A_3 cannot also be zero (or else there is no particle; psi(x)=0). The
only way for the equation to always be zero is if the sin term is always zero. This only occurs when k*a is some
integer multiple of pi
Note that if k = 0, then the sin(kx) term is always zero, and hence (just like if A_3 = 0), the whole wave function term is just zero. This would mean that there is no particle present at all (a possibility, but trivial to note).
To find the constant A_3, let us normalize the wave function:
In order to make sure everyone is following, let us review some key steps below:
14: Finding the normalization of the wave function. An integral is a sum and the function is zero outside the box. This
means that the bounds from -infinity to infinity can reduce to 0 to a.
14 to 15: Pull A_3 outside the integral as it is just a constant
15 to 16: Solve the integral and set it equal to 1. We now have the constant in terms of known quantities (box's size)
It is important to note that we solved for the magnitude of A_3. Therefore, the most general from for A_3 can be written as:
14: Finding the normalization of the wave function. An integral is a sum and the function is zero outside the box. This
means that the bounds from -infinity to infinity can reduce to 0 to a.
14 to 15: Pull A_3 outside the integral as it is just a constant
15 to 16: Solve the integral and set it equal to 1. We now have the constant in terms of known quantities (box's size)
It is important to note that we solved for the magnitude of A_3. Therefore, the most general from for A_3 can be written as:
Before we put all the pieces together, let us first sole for the energy of the particle:
Let us stop and take a few notes about the energy equation. First: energy can NEVER be zero. If energy is zero, then the wave function is zero and there is no particle. Second: energy is QUANTIZED!! Just like for a free particle, the particle cannot exist at any energy level. Physically this means that an electron excited to another energy state does NOT go through every possible energy value in between, but rather jumps immediately to that new energy state. You cannot half excite an electron (it cannot exist in between two energy states). We need the full and exact amount of energy to make it there. Mathematically this quantization arises because the energy relates to the wave function, which is constrained by the boundary conditions (it has to go to zero at certain points)
We can now solve the full time dependent Schrödinger equation below:
We can now solve the full time dependent Schrödinger equation below:
|
|
|