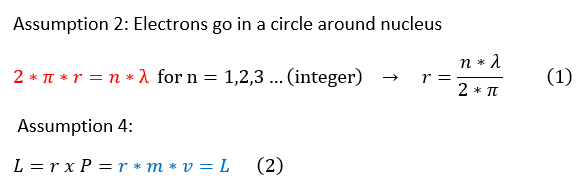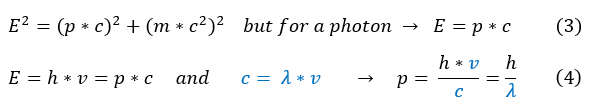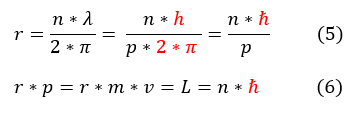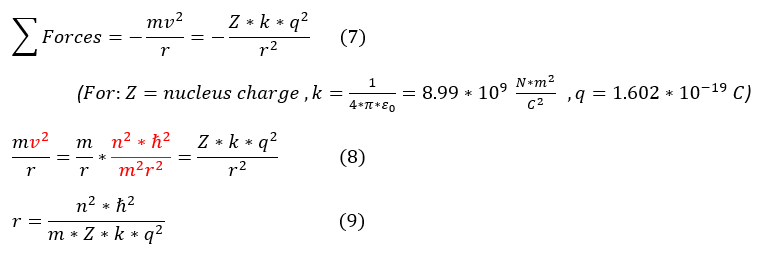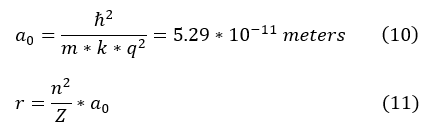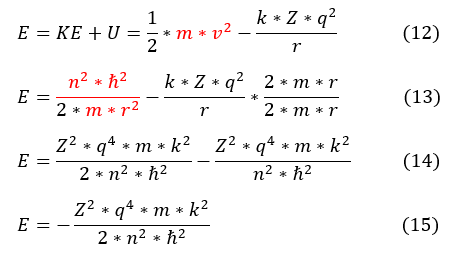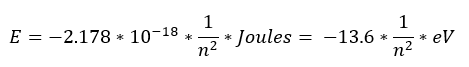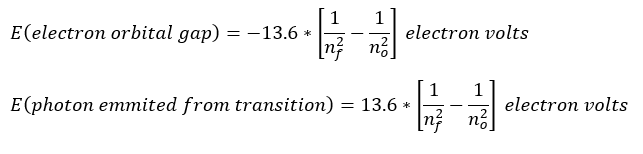Mind Network - Samuel Solomon
Bohr Model of the Atom
The photoelectric effect, Compton scatter, and black body radiation taught physicists something: the man-written rules of physics must be edited. One of the first attempts was made by Niels Bohr. In order to start this new age in physics, he decided to make his own atomic model. Here are the key assumptions:
1. Electrons move in circular orbits
2. Bound electrons are standing waves
3. Energy of photon's are quantized, with energy gaps = h*v.
4. Electron's orbit around the nucleus with an angular momentum of L = r x P
Let us now analyze the physics of assumptions 2 and 4.
1. Electrons move in circular orbits
2. Bound electrons are standing waves
3. Energy of photon's are quantized, with energy gaps = h*v.
4. Electron's orbit around the nucleus with an angular momentum of L = r x P
Let us now analyze the physics of assumptions 2 and 4.
Now it is important to introduce a new topic in quantum mechanics. It is called the de Broglie relationship (which was presented as his thesis ... I can only imagine the thesis review that occurred...). It states that all matter has an associative wavelength and all waves have an associated mass. The simple proof (yes very simple) can be found below.
In order to make sure everyone is following, let us review some key steps below:
3: Start from our previous general energy relationship for particles; however, photon's are massless.
4: Set out planck's energy and general energy equal to each other. Solve for the de Broglie relation.
Let us now plug this relation (4) back into our equation 1.
3: Start from our previous general energy relationship for particles; however, photon's are massless.
4: Set out planck's energy and general energy equal to each other. Solve for the de Broglie relation.
Let us now plug this relation (4) back into our equation 1.
In order to make sure everyone is following, let us review some key steps below:
5: Take equation 1 and plug out de Broglie relationship into the equation. Additionally used a new h_bar symbol.
6: Added equation 2 into the mix. Found a new equation for angular momentum.
The significance of this calculation is that (while some of the assumptions are inaccurate) it is the first postulate that angular momentum of particles is quantized just like energy. Only certain angular momentum values are allowed and again it is some integer multiple (divided by 2*pi) of this strange constant h.
Let us continue and now use these principles on the hydrogen atom (ie one electron orbiting one nucleus). The first thing we are going to do is go back to Newton's second law for orbiting particles:
5: Take equation 1 and plug out de Broglie relationship into the equation. Additionally used a new h_bar symbol.
6: Added equation 2 into the mix. Found a new equation for angular momentum.
The significance of this calculation is that (while some of the assumptions are inaccurate) it is the first postulate that angular momentum of particles is quantized just like energy. Only certain angular momentum values are allowed and again it is some integer multiple (divided by 2*pi) of this strange constant h.
Let us continue and now use these principles on the hydrogen atom (ie one electron orbiting one nucleus). The first thing we are going to do is go back to Newton's second law for orbiting particles:
In order to make sure everyone is following, let us review some key steps below:
7: Newton's second law for orbiting particles = sum(forces) = electrostatic force of the electron and nucleus.
7 to 8: plug in equation 6 (without angular momentum) for velocity.
8 to 9: simplify the expression.
While this radial distance of the electron looks daunting, it actually is composed of essentially constants. We can therefore define a useful constant below (called the Bohr radius):
7: Newton's second law for orbiting particles = sum(forces) = electrostatic force of the electron and nucleus.
7 to 8: plug in equation 6 (without angular momentum) for velocity.
8 to 9: simplify the expression.
While this radial distance of the electron looks daunting, it actually is composed of essentially constants. We can therefore define a useful constant below (called the Bohr radius):
Now that one has found the equilibrium radius of an electron calculated by Bohr (which is wrong for basically all cases but 1), it is time to determine the theoretical energy.
Total energy is the sum of kinetic and potential energy.
Total energy is the sum of kinetic and potential energy.
In order to make sure everyone is following, let us review some key steps below:
12 to 13: Plugged in the equation 6 (without angular momentum) for velocity. Also made both denominators equal.
13 to 14: Replaced the r^2 of each term with the one we solved for in equation 9.
14 to 15: Simplified the expression.
Again, a lot of these terms are constants, so let's plug in those true values to get:
12 to 13: Plugged in the equation 6 (without angular momentum) for velocity. Also made both denominators equal.
13 to 14: Replaced the r^2 of each term with the one we solved for in equation 9.
14 to 15: Simplified the expression.
Again, a lot of these terms are constants, so let's plug in those true values to get:
This is a great approximation of the energy gaps in the Hydrogen atom (where Z = 1) and a good takeaway from the Bohr model. It was very coincidental that this is a good model (given the false starting assumptions), but we will be able to go and develop a better equation for Hydrogen through our quantum mechanical expressions.
The last note about this equation is that the plus and minus sign are very case dependent as follows:
The last note about this equation is that the plus and minus sign are very case dependent as follows:
|
|
|