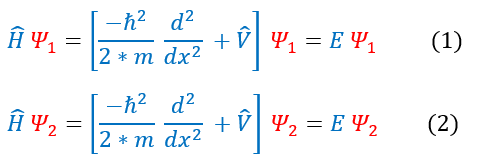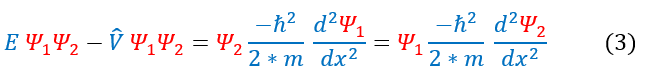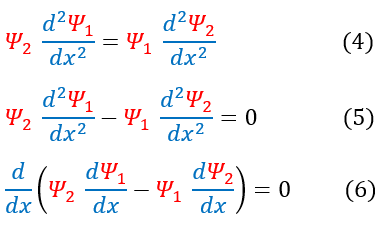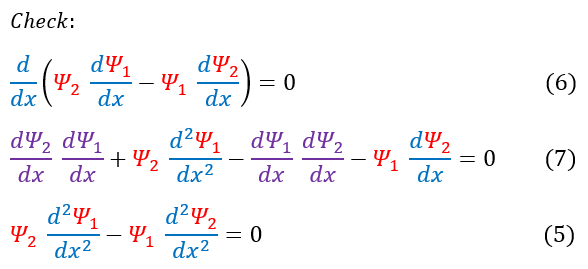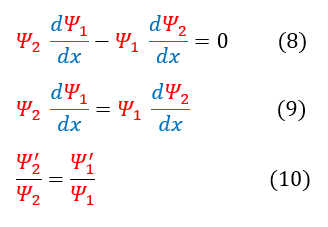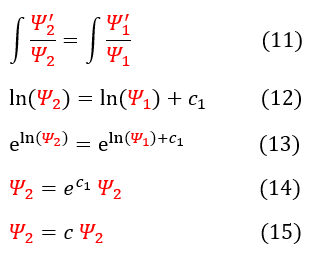Mind Network - Samuel Solomon
No Degeneracy in 1-Dimension
The Schrödinger equation can be solved for a given potential V(r); however, there is still one more variable we have to input: the total energy. The total energy of a closed system (which is how we tend to pick our systems) is a constant and different energies will lead to different wave functions (think about a wave on a string: higher the frequency / different wave equation = more nodes = higher energy). However, one might start to wonder if the opposite is still true: can different wave functions lead to the same energy? The answer is yes! We call such a case a degeneracy.
Degenerate states are defined to be different wave functions that all have the exact same energy. We will indeed come across such a system in 3-dimensions. However, in this page, I want to prove to you that although it is possible in 3-D, we CANNOT have a degenerate wave function in 1-dimension.
To begin this proof, let us suppose we actually did have two degenerate 1-D states in the same potential (in the same system). Each wave function would be different, but their potential field and energies would be the same. They would both have to solve the position-dependent Schrödinger equation. We can represent this below:
Degenerate states are defined to be different wave functions that all have the exact same energy. We will indeed come across such a system in 3-dimensions. However, in this page, I want to prove to you that although it is possible in 3-D, we CANNOT have a degenerate wave function in 1-dimension.
To begin this proof, let us suppose we actually did have two degenerate 1-D states in the same potential (in the same system). Each wave function would be different, but their potential field and energies would be the same. They would both have to solve the position-dependent Schrödinger equation. We can represent this below:
In order to equate the two formulas, we can multiple equation 1 by psi_2 and equation 2 by psi_1. This will give us:
Equation 3 has a lot of symmetry. We can further manipulate this symmetry below:
In order to make sure everyone is following, let us review some key steps below:
4: Simplify the expression in equation 3
4 to 5: Pull the RHS term over to the LHS
5 to 6: We can notice the symmetry of equation 5. Using this symmetry, we pull out one derivative term
In order to make sure everyone understands: I provided a check on the right (going from equation 6 back to equation 5)
As one may be able to see in equation 6, the whole expression inside of the parenthesis must be a constant with respect to x (as the derivative is zero). It should be a constant regardless of which x-value we choose to evaluate the derivative. We know that the wave function must decay at +/- infinity. Hence, when you evaluate the derivatives at +/- infinity, both of the derivatives should go to zero / be the same small number (as the slope of the wave function should decay to zero). Because the constant equals zero at one point, and it is a constant with respect to the x-value chosen, we know that the term inside the parenthesis MUST BE ZERO.
Another note for those familiar with matrix mechanics (specifically differential equations), we call this inside expression ( at least the general form) the Wronskian. However, that definition is irrelevant for this proof.
All of this aside, we can continue on with our proof, setting the inside function in equation 6 to zero:
4: Simplify the expression in equation 3
4 to 5: Pull the RHS term over to the LHS
5 to 6: We can notice the symmetry of equation 5. Using this symmetry, we pull out one derivative term
In order to make sure everyone understands: I provided a check on the right (going from equation 6 back to equation 5)
As one may be able to see in equation 6, the whole expression inside of the parenthesis must be a constant with respect to x (as the derivative is zero). It should be a constant regardless of which x-value we choose to evaluate the derivative. We know that the wave function must decay at +/- infinity. Hence, when you evaluate the derivatives at +/- infinity, both of the derivatives should go to zero / be the same small number (as the slope of the wave function should decay to zero). Because the constant equals zero at one point, and it is a constant with respect to the x-value chosen, we know that the term inside the parenthesis MUST BE ZERO.
Another note for those familiar with matrix mechanics (specifically differential equations), we call this inside expression ( at least the general form) the Wronskian. However, that definition is irrelevant for this proof.
All of this aside, we can continue on with our proof, setting the inside function in equation 6 to zero:
In order to make sure everyone is following, let us review some key steps below:
8: The constant function from equation 6. From evaluating it at +/- infinity, we know that this constant is zero
8 to 9: Move on of the terms over to the other side
9 to 10: divide both sides by psi(1) and psi(2). We are now using the prime (') notation to represent the derivative
10 to 11: Since both of the functions are equal, so are their integrals (up to a constant)
11 to 12: Evaluate the integrals
12 to 13: Put both sides in the exponent of 'e'
13 to 14: Simplify the expression. We note that e^(ln(x))=x
14 to 15: Note, e^constant = constant. We rename this constant c
From equation 15, we note that psi(1) is just a scalar multiple of psi(2). The scalar amount is actually irrelevant because we must normalize all wave functions to 1. Hence, when normalized, psi(1) will equal psi(2). They are actually the EXACT same wave function. For 1-dimension, we CANNOT have degenerate states. This proof does not extend to 3-dimensions though (when there is a psi(x), psi(y), and psi(z) in the same equation).
8: The constant function from equation 6. From evaluating it at +/- infinity, we know that this constant is zero
8 to 9: Move on of the terms over to the other side
9 to 10: divide both sides by psi(1) and psi(2). We are now using the prime (') notation to represent the derivative
10 to 11: Since both of the functions are equal, so are their integrals (up to a constant)
11 to 12: Evaluate the integrals
12 to 13: Put both sides in the exponent of 'e'
13 to 14: Simplify the expression. We note that e^(ln(x))=x
14 to 15: Note, e^constant = constant. We rename this constant c
From equation 15, we note that psi(1) is just a scalar multiple of psi(2). The scalar amount is actually irrelevant because we must normalize all wave functions to 1. Hence, when normalized, psi(1) will equal psi(2). They are actually the EXACT same wave function. For 1-dimension, we CANNOT have degenerate states. This proof does not extend to 3-dimensions though (when there is a psi(x), psi(y), and psi(z) in the same equation).
|
|
|