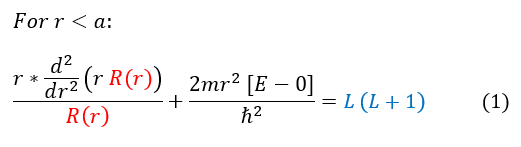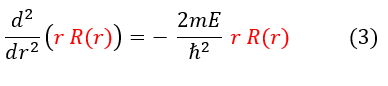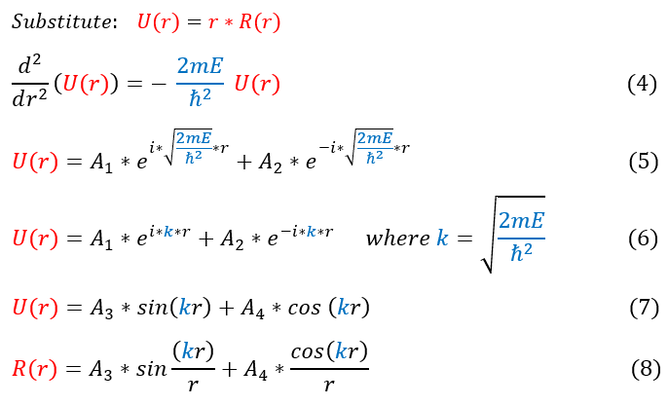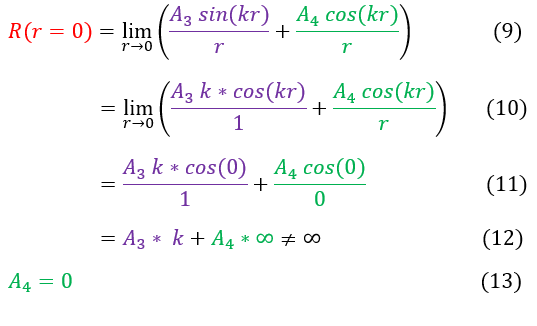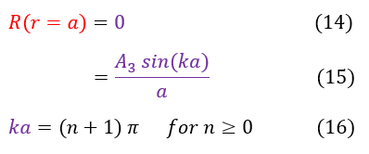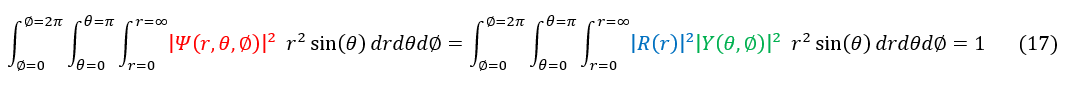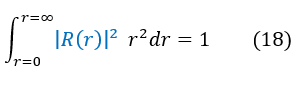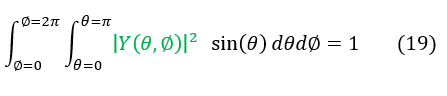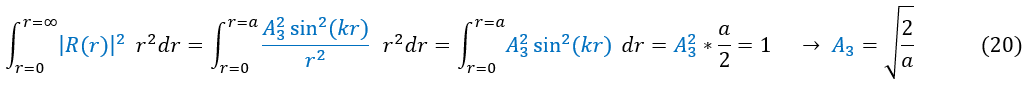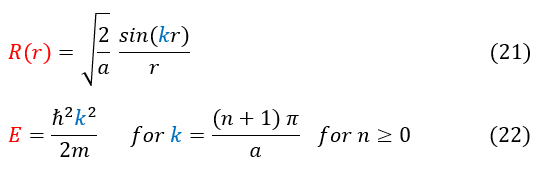Mind Network - Samuel Solomon
Infinite Spherical Well
Radial Solution
|
|
|
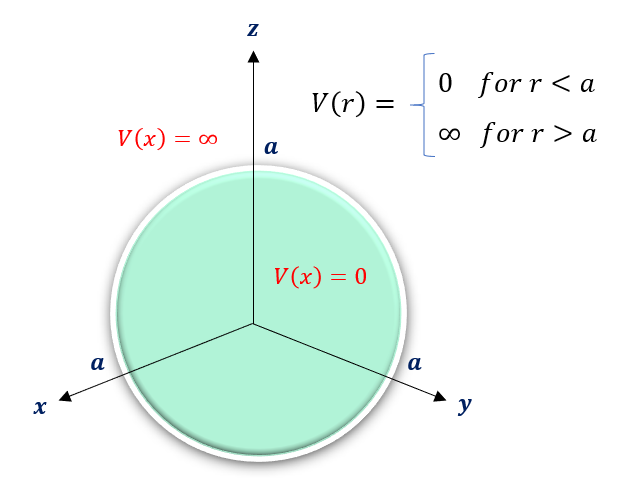
The easiest spherically symmetric potential to solve is the infinite spherical well: potential equals zero inside a sphere and infinity outside the sphere.
The potential energy diagram as well as our spherical coordinate definitions are defined below:
The potential energy diagram as well as our spherical coordinate definitions are defined below:
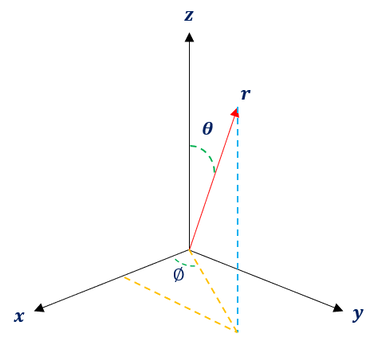
It is important to note that even among scientists, people tend to define these coordinates differently. But as long as we are internally consistent, it is okay. To be clear, my coordinates are defined as follows:
Theta: The angle the point makes with the z axis
Phi: The angle the point makes with the x-axis in the x-y plane
r: the distance between the point and the origin (Some call it 'Rho')
We are now ready to solve our radial Schrödinger equation for the infinite spherical well below:
Theta: The angle the point makes with the z axis
Phi: The angle the point makes with the x-axis in the x-y plane
r: the distance between the point and the origin (Some call it 'Rho')
We are now ready to solve our radial Schrödinger equation for the infinite spherical well below:
Equation 2 has an infinity term and hence cannot be solved. The equation can only hold, for any radial wave function, if R(r) is zero (just like 'particle in a box'). This leaves us to solve R(r) equation (1) for inside the spherical well (with the intention of patching the two solutions together in the end).
To solve the radial equation inside the well, we should first define an angular momentum value 'L' (though not required, it does ground the problem more). While we can define any 'L' value to solve mathematically, but for our sake let us choose 'L' = 0, which would correspond to an S orbital (though not discussed just yet). Note: S orbitals do not have a potential of infinity outside the well and zero inside the well, so the analogy does fall short a little here. Think of this more as a first step / intuition on the long mathematical road to get to the real S orbital wave function.
Our radial equation for a spherically symmetric potential in an infinite square well with L = 0 can now be written as:
To solve the radial equation inside the well, we should first define an angular momentum value 'L' (though not required, it does ground the problem more). While we can define any 'L' value to solve mathematically, but for our sake let us choose 'L' = 0, which would correspond to an S orbital (though not discussed just yet). Note: S orbitals do not have a potential of infinity outside the well and zero inside the well, so the analogy does fall short a little here. Think of this more as a first step / intuition on the long mathematical road to get to the real S orbital wave function.
Our radial equation for a spherically symmetric potential in an infinite square well with L = 0 can now be written as:
To solve this equation, we will use the u-substitution method where u = r * R(r). This will leave us with:
In order to make sure everyone is following, let us review some key steps below:
4: Add in our u-substitution to equation 3
4 to 5: Solve the differential equation
5 to 6: Rewrite the equation with the constant 'k'
6 to 7: Use Euler's equation to write e^ikx in terms of cosines and sines
7 to 8: Plug back in our initial expression U(r) = r * R(r)
We are now ready to apply our boundary conditions to the problem:
1. The wave function must be continuous at r = 0
2. The wave function must be continuous at r = a
Because we have an infinite potential barrier, the slope of the wave function does not matter at r = a
4: Add in our u-substitution to equation 3
4 to 5: Solve the differential equation
5 to 6: Rewrite the equation with the constant 'k'
6 to 7: Use Euler's equation to write e^ikx in terms of cosines and sines
7 to 8: Plug back in our initial expression U(r) = r * R(r)
We are now ready to apply our boundary conditions to the problem:
1. The wave function must be continuous at r = 0
2. The wave function must be continuous at r = a
Because we have an infinite potential barrier, the slope of the wave function does not matter at r = a
We can solve for A_3 by normalizing the wave function:
Equation 17 represents the full normalization equation for spherical coordinates (the integral over all space). However, we are only solving for the radial component in this problem. This is no worry; normalization is just a constant. We can break up equation 17 into two different normalizations below:
If equation 18 AND equation 19 normalize to 1, then by definition equation 17 would as well (think 1*1=1). We can therefore normalize our radial equation using equation 18 below:
And with that we have solved the radial component of the infinite spherical well. Altogether, the solution looks like:
|
|
|