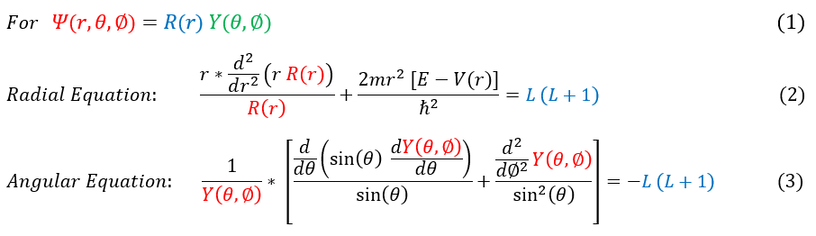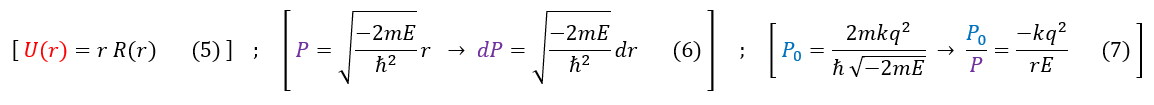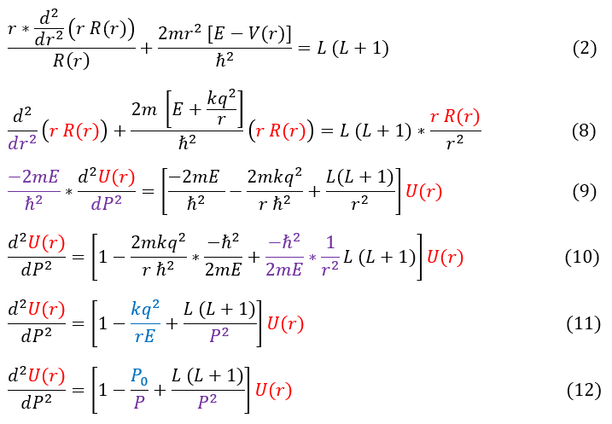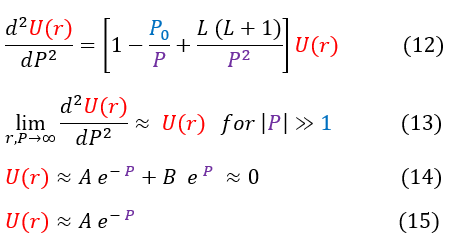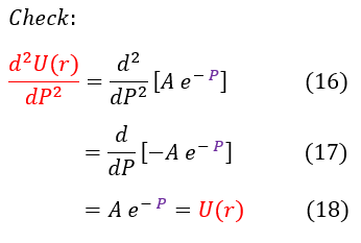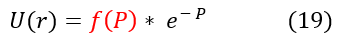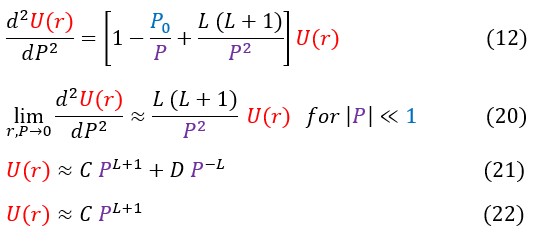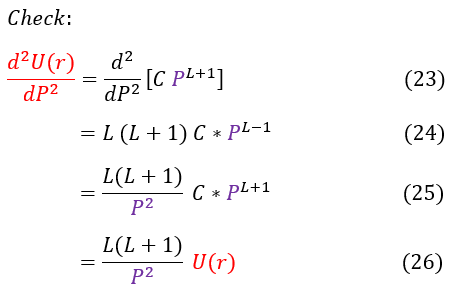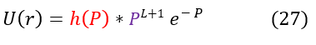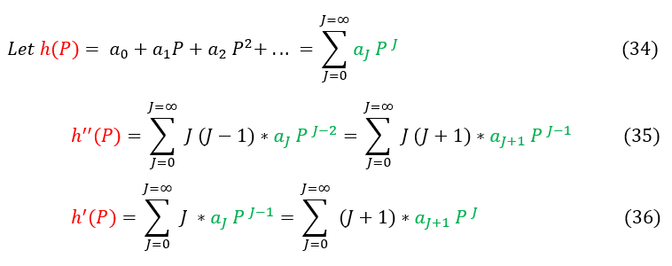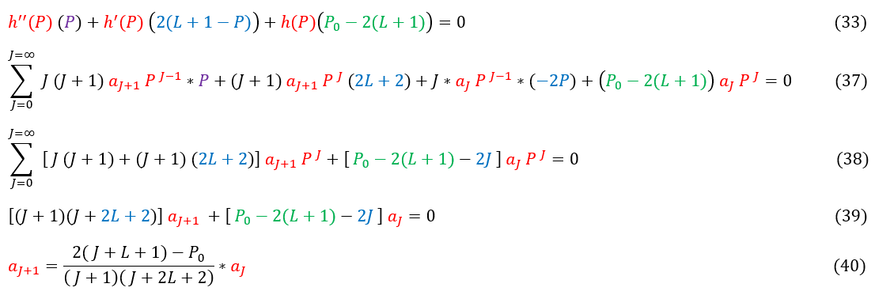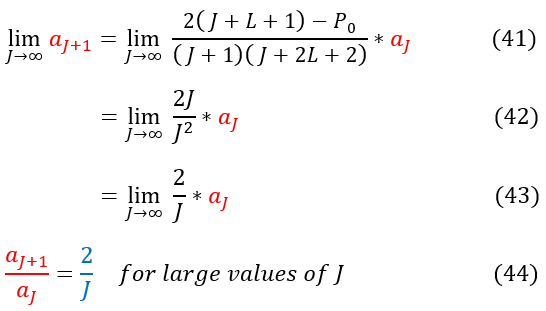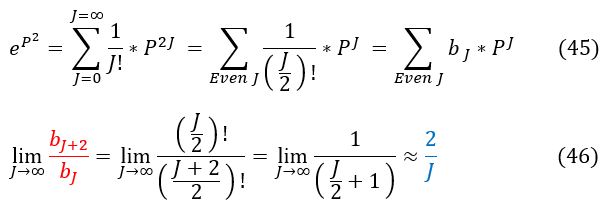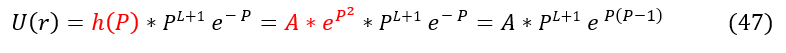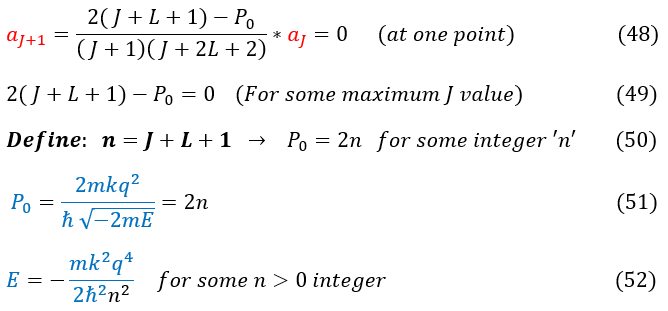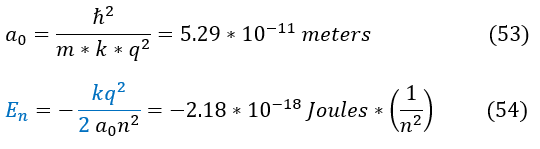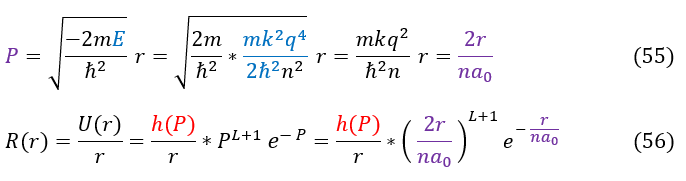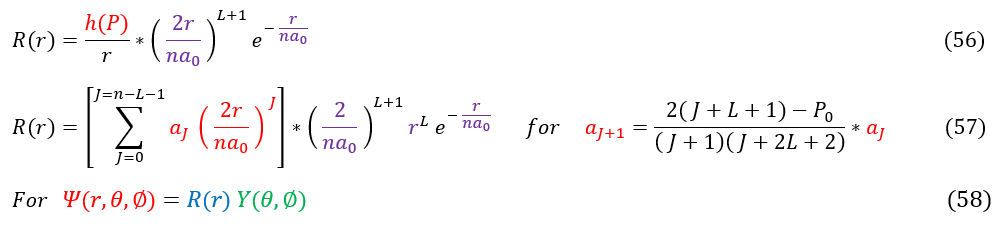Mind Network - Samuel Solomon
Hydrogen Atom
Radial Solution; Any Orbital
|
|
|
In the last page, we have solved the angular solution to the Schrödinger equation for any spherically symmetric potential for any 'L' quantum number. This included the Hydrogen atom's angular solution (the spherical harmonics). In order to finish off our quantum mechanics solution of the Hydrogen atom, we also need to solve the radial component. As a reminder, the two Schrödinger equations for spherically symmetric potentials were as follows:
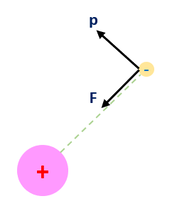
We did not need to define a potential to solve for the angular solution, but we will need to define a potential for the radial component. A one electron atom, like the Hydrogen atom, consists of only a nucleus and a sole electron. The electron is held (bounded) by the nucleus by an electrostatic interaction (a radial force). Our quantum picture of this system is diagrammed below:
Where k = Coulomb constant; Z = nuclear charge (Hydrogen: Z = +1); q = magnitude of charge (for one electron or proton)
In the diagram, we only show the electron moving. This is because the nuclear mass is much bigger than the electron's mass, and hence, for the same force, the electron accelerates and moves a lot more. It moves so much, that the nuclear movements are rather negligible in comparison (we don't really see the nucleus move that much). We call this the Born-Oppenheimer approximation (and sometimes the Franck-Condon limit depending on your field). Regardless, the Schrödinger equation does not differentiate on this basis, but I thought I would point this out.
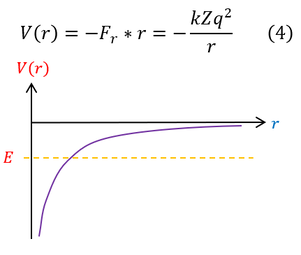
What is important to solve is the Schrödinger equation and for that all we need is the potential energy. From non-relativistic electromagnetism, we know the force and potential energy exerted on two charged particles (shown in the above diagram on the right), and hence also know the potential energy.
For a quick check, we can see that the electrostatic forces are radial forces, which produces a spherically symmetric potential (which we assumed in equation 2). Therefore, we are now ready to solve the radial Schrödinger equation for the Hydrogen atom. It will be a mathematically challenging proof, so we will make 3 simplifying substitutions to our radial wave equation first:
In the diagram, we only show the electron moving. This is because the nuclear mass is much bigger than the electron's mass, and hence, for the same force, the electron accelerates and moves a lot more. It moves so much, that the nuclear movements are rather negligible in comparison (we don't really see the nucleus move that much). We call this the Born-Oppenheimer approximation (and sometimes the Franck-Condon limit depending on your field). Regardless, the Schrödinger equation does not differentiate on this basis, but I thought I would point this out.
What is important to solve is the Schrödinger equation and for that all we need is the potential energy. From non-relativistic electromagnetism, we know the force and potential energy exerted on two charged particles (shown in the above diagram on the right), and hence also know the potential energy.
For a quick check, we can see that the electrostatic forces are radial forces, which produces a spherically symmetric potential (which we assumed in equation 2). Therefore, we are now ready to solve the radial Schrödinger equation for the Hydrogen atom. It will be a mathematically challenging proof, so we will make 3 simplifying substitutions to our radial wave equation first:
We can now plug these into the radial equation (equation 2):
In order to make sure everyone is following, let us review some key steps below:
2: The radial Schrödinger equation for any 'L' quantum number
2 to 8: Multiply both sides by R(r) and divide by 'r.' We also plugged in our Hydrogen atom potential for V(r)
8 to 9: Replace the red 'r R(r)' with 'U(r)' and the purple 'dr^2' with 'dP^2' (also moved the U(r) terms onto the RHS)
9 to 10: Divide out the purple term
10 to 11: Simplify the middle term on the right and repalce the purple term with 1/P^2 (equation 6)
11 to 12: Replace the blue middle term on the RHS with 'P_0/P' (equation 7)
Now this differential equation in line 12 is less of a headache to solve (don't have to worry about tons of constants). In order to solve it, like any other differential equations, we need an ansatz (a trial function). In order to have a good anstaz, lets first get a general sense of the solution by looking at its extreme values (limiting cases): we know that as r (and by extension P) goes to infinity, the wave function R(r) (and by extension U(r)) must go to zero. We can evaluate this limit below:
2: The radial Schrödinger equation for any 'L' quantum number
2 to 8: Multiply both sides by R(r) and divide by 'r.' We also plugged in our Hydrogen atom potential for V(r)
8 to 9: Replace the red 'r R(r)' with 'U(r)' and the purple 'dr^2' with 'dP^2' (also moved the U(r) terms onto the RHS)
9 to 10: Divide out the purple term
10 to 11: Simplify the middle term on the right and repalce the purple term with 1/P^2 (equation 6)
11 to 12: Replace the blue middle term on the RHS with 'P_0/P' (equation 7)
Now this differential equation in line 12 is less of a headache to solve (don't have to worry about tons of constants). In order to solve it, like any other differential equations, we need an ansatz (a trial function). In order to have a good anstaz, lets first get a general sense of the solution by looking at its extreme values (limiting cases): we know that as r (and by extension P) goes to infinity, the wave function R(r) (and by extension U(r)) must go to zero. We can evaluate this limit below:
In order to make sure everyone is following, let us review some key steps below:
12: Our equation we are trying to solve
12 to 13: We take the limit of the equation as r (or P) goes to infinity (1/P is now essentially zero)
13 to 14: We solve the differential equation
14 to 15: As P goes to infinity, U(r) must go to zero, which cannot happen with the 'e^P' term; hence, B must be zero
We do a quick mathematical check on the right to make sure we solved the differential equation correctly.
We now have a general idea of how the solution acts as 'r' or 'P' goes to +/- infinity. As 'P' goes to +/- infinity, the exponential term in equation 15 dominates the value of U(r). However, as 'P' becomes smaller and smaller, the co-factor 'A' is no longer an insignificant value. While it may have acted like a constant in the limit, it could possibly vary with 'P.' We can account for that in our new general ansatz below:
12: Our equation we are trying to solve
12 to 13: We take the limit of the equation as r (or P) goes to infinity (1/P is now essentially zero)
13 to 14: We solve the differential equation
14 to 15: As P goes to infinity, U(r) must go to zero, which cannot happen with the 'e^P' term; hence, B must be zero
We do a quick mathematical check on the right to make sure we solved the differential equation correctly.
We now have a general idea of how the solution acts as 'r' or 'P' goes to +/- infinity. As 'P' goes to +/- infinity, the exponential term in equation 15 dominates the value of U(r). However, as 'P' becomes smaller and smaller, the co-factor 'A' is no longer an insignificant value. While it may have acted like a constant in the limit, it could possibly vary with 'P.' We can account for that in our new general ansatz below:
Just like for the quantum harmonic oscillator and the one-electron atom case, we could keep going to solve for this function f(P). However, one will find this extremely difficult ... our ansatz isn't good enough just yet (this is just my foresight into the problem; with a lot of pain it probably can still be solved). To add more information to our ansatz (our guess function), let us also evaluate U(r) as 'r' or 'P' goes to zero. While we do not know this specific value, we do know that it has to be a finite number (we can never diverge to infinity or the area under the curve won't be finite / normalizable). We can evaluate this boundary below:
In order to make sure everyone is following, let us review some key steps below:
12: Our equation we are trying to solve
12 to 20: We take the limit of the equation as r (or P) goes to zero
20 to 21: We solve the differential equation
21 to 22: As P goes to zero, U(r) must be finite, which cannot happen with the 'P^-L' term (~1/0); hence, D must be zero
We do a quick mathematical check on the right to make sure we solved the differential equation correctly.
We now have a general idea of how the solution acts as 'r' or 'P' goes to +/- infinity AND as 'r' or 'P' goes to zero. Using this combined understanding of how the function is supposed to look like, we can make an even better educated guess (ansatz) for what U(r) should be. As 'P' goes to +/- infinity, the exponential term in equation 15 dominates the value of U(r) and as 'P' goes to zero the P^(L+1) term dominates. We can account for that in our new general ansatz below:
12: Our equation we are trying to solve
12 to 20: We take the limit of the equation as r (or P) goes to zero
20 to 21: We solve the differential equation
21 to 22: As P goes to zero, U(r) must be finite, which cannot happen with the 'P^-L' term (~1/0); hence, D must be zero
We do a quick mathematical check on the right to make sure we solved the differential equation correctly.
We now have a general idea of how the solution acts as 'r' or 'P' goes to +/- infinity AND as 'r' or 'P' goes to zero. Using this combined understanding of how the function is supposed to look like, we can make an even better educated guess (ansatz) for what U(r) should be. As 'P' goes to +/- infinity, the exponential term in equation 15 dominates the value of U(r) and as 'P' goes to zero the P^(L+1) term dominates. We can account for that in our new general ansatz below:
Where h(P) is some function of 'P' we don't know yet. We can now plug back in our ansatz to equation 12 to solve for the explicit form of h(P)
In order to make sure everyone is following, let us review some key steps below:
28: Plug our ansatz into equation 12
28 to 30: Working with the middle term, take the first and second derivative of the ansatz (simplified it as well)
30 to 31: Reshow the RHS of equation 28
31: Combine the LHS (equation 30) and the RHS (equation 31). We cancel out the 'P^L * e^-P' terms
32 to 33: Simplify the expression
We now have a second order differential equation for the h(P) function. In order to solve a differential equation (just like before) we need another ansatz. This time, we will expand out h(P) into a polynomial series (see power series for reference). For those unfamiliar with this trick, it is the same principle of Taylor series. We will show this below:
28: Plug our ansatz into equation 12
28 to 30: Working with the middle term, take the first and second derivative of the ansatz (simplified it as well)
30 to 31: Reshow the RHS of equation 28
31: Combine the LHS (equation 30) and the RHS (equation 31). We cancel out the 'P^L * e^-P' terms
32 to 33: Simplify the expression
We now have a second order differential equation for the h(P) function. In order to solve a differential equation (just like before) we need another ansatz. This time, we will expand out h(P) into a polynomial series (see power series for reference). For those unfamiliar with this trick, it is the same principle of Taylor series. We will show this below:
In order to make sure everyone is following, let us review some key steps below:
34: The definition of a power series
35 and 36: We apply the derivatives on the power series. We also reformat the indeces (see below)
Note the switch in indeces for equations 35 and 26. We do this because when J = 0 we are adding zero in our sum (which is trivial). We therefore skip over this index in the summation (as it is just adding in zero). In order to do this, we add 1 to ever J term.
Let us now plug this ansatz into equation 33 to solve for the 'a_J' terms in the polynomial expansion of h(P):
34: The definition of a power series
35 and 36: We apply the derivatives on the power series. We also reformat the indeces (see below)
Note the switch in indeces for equations 35 and 26. We do this because when J = 0 we are adding zero in our sum (which is trivial). We therefore skip over this index in the summation (as it is just adding in zero). In order to do this, we add 1 to ever J term.
Let us now plug this ansatz into equation 33 to solve for the 'a_J' terms in the polynomial expansion of h(P):
In order to make sure everyone is following, let us review some key steps below:
33: Our differential equation we need to solve for h(P)
37: Plug in our power series expansion of h(P). Note: I split the h'(P) terms. My goal is to eventually pull out 'P^J'
37 to 38: Group the terms by 'a_J+1' and 'a_J.' I additionally pull out a 'P^J' term.
38 to 39: 'P' (a function of 'r') spans from +/- infinity. Hence, its coefficient must sum to zero at all 'P' values / indeces
39 to 40: Solve for 'a_j+1' in terms of 'a_j'
Some mathematicians might immediately see the problem with equation 40. However, it is not immediately obvious, so lets make it clear. Let us look at the limiting case as J goes to infinity (the terms near the end of the summation):
33: Our differential equation we need to solve for h(P)
37: Plug in our power series expansion of h(P). Note: I split the h'(P) terms. My goal is to eventually pull out 'P^J'
37 to 38: Group the terms by 'a_J+1' and 'a_J.' I additionally pull out a 'P^J' term.
38 to 39: 'P' (a function of 'r') spans from +/- infinity. Hence, its coefficient must sum to zero at all 'P' values / indeces
39 to 40: Solve for 'a_j+1' in terms of 'a_j'
Some mathematicians might immediately see the problem with equation 40. However, it is not immediately obvious, so lets make it clear. Let us look at the limiting case as J goes to infinity (the terms near the end of the summation):
In order to make sure everyone is following, let us review some key steps below:
41: Finding 'a_J+1' for large values of 'J' (as J goes to infinity)
41 to 42: Constants in the numerator and order(1) terms in the denominator are insignificant in the limit
42 to 43: Simplify the expression
43 to 44: We find The ratio of 'a_j+1' to ''a_j' to be 2/J
We can compare this answer to the expression on the right:
45: We can Taylor expand exp(P^2) into a format that matches the power series starting equation (for 'b' instead of 'a')
45 to 46: Now when we take the ratio, in the limit as J goes to infinity, we again find the same ratio 2/J
For very large 'J' values, our expression in equation 40 acts like exp(P^2). This is NOT good because, going back to the beginning, we MUST have the wave function normalize. If h(P) has an exp(P^2) term then:
41: Finding 'a_J+1' for large values of 'J' (as J goes to infinity)
41 to 42: Constants in the numerator and order(1) terms in the denominator are insignificant in the limit
42 to 43: Simplify the expression
43 to 44: We find The ratio of 'a_j+1' to ''a_j' to be 2/J
We can compare this answer to the expression on the right:
45: We can Taylor expand exp(P^2) into a format that matches the power series starting equation (for 'b' instead of 'a')
45 to 46: Now when we take the ratio, in the limit as J goes to infinity, we again find the same ratio 2/J
For very large 'J' values, our expression in equation 40 acts like exp(P^2). This is NOT good because, going back to the beginning, we MUST have the wave function normalize. If h(P) has an exp(P^2) term then:
exp(P^2-P) does NOT normalize and cannot be how our equation acts as P (or r) goes to +/- infinity.
The only way to mathematically get around this fact is if we NEVER sum up these diverging terms at all. We need our summation to converge (as our wave function should never diverge to infinity); hence, we need 'a_j+1' to go to zero at one point. Once 'a_j+1' = 0 at one point, then the rest of the terms in the infinite summation also equals zero and the finite summation will converge (not go to infinity and we will not see these diverging terms)
The only way to mathematically get around this fact is if we NEVER sum up these diverging terms at all. We need our summation to converge (as our wave function should never diverge to infinity); hence, we need 'a_j+1' to go to zero at one point. Once 'a_j+1' = 0 at one point, then the rest of the terms in the infinite summation also equals zero and the finite summation will converge (not go to infinity and we will not see these diverging terms)
In order to make sure everyone is following, let us review some key steps below:
48: Equation 40 (relationship between 'a' coefficients in the power series). For some J_max, 'a_j+1' must be zero
48 to 49: In order for this to be true, the numerator must be zero for some J_max (end of summation) value
49 to 50: Define a new constant 'n' to be J+L+1. 'J' and 'L' are integers so 'n' is also an integer
50 to 51: P_0 was a constant we defined in the beginning of the problem. We now plug back in its original value
51 to 52: Solve for the energy 'E'
NOTE: we initially stated that J (or n) started from zero. Now we know that n can actually never be zero, and the index really starts at n = 1 (we didn't know this initially, so I included the index in equations 26 - 28). We can't have 1/0.Note that the 'n' values only go up to some 'n_max.'
And that is the energy of the Hydrogen atom. There are two very important notes about this energy:
1. Bohr got this EXACT SAME result earlier by just considering the electron as a standing wave going in a circle
2. The angular momentum 'L' quantum number does NOT effect the energy. Only the 'n' value
2. The energy of the Hydrogen atom is QUANTIZED (cannot take on certain energy values; constrained by 'n')
This energy quantization mathematically arose because of the necessity for the series to converge (for the wave function to be normalized). Because not all wave functions normalize, not all energies are possible (remember, this is similar to the particle in a box situation / energy quantization).
A quick note about the Bohr model: it is wrong. Electrons do not just go in a 2D circle around the nucleus. It is crazy (lucky) that Bohr actually got the right answer. This is why the Bohr model was so famous. Before people could really comprehend this mathematically, somehow Bohr was telling people the right answers for their experimental results. It had some things to do with luck, but Bohr did use quantization of angular momentum (which back then, like now, was hard for people to think about). So Bohr's model did get some things right (and was very novel to think of). Going back to the Bohr model, Bohr defined a very useful constant: the Bohr radius. We can use this constant below:
48: Equation 40 (relationship between 'a' coefficients in the power series). For some J_max, 'a_j+1' must be zero
48 to 49: In order for this to be true, the numerator must be zero for some J_max (end of summation) value
49 to 50: Define a new constant 'n' to be J+L+1. 'J' and 'L' are integers so 'n' is also an integer
50 to 51: P_0 was a constant we defined in the beginning of the problem. We now plug back in its original value
51 to 52: Solve for the energy 'E'
NOTE: we initially stated that J (or n) started from zero. Now we know that n can actually never be zero, and the index really starts at n = 1 (we didn't know this initially, so I included the index in equations 26 - 28). We can't have 1/0.Note that the 'n' values only go up to some 'n_max.'
And that is the energy of the Hydrogen atom. There are two very important notes about this energy:
1. Bohr got this EXACT SAME result earlier by just considering the electron as a standing wave going in a circle
2. The angular momentum 'L' quantum number does NOT effect the energy. Only the 'n' value
2. The energy of the Hydrogen atom is QUANTIZED (cannot take on certain energy values; constrained by 'n')
This energy quantization mathematically arose because of the necessity for the series to converge (for the wave function to be normalized). Because not all wave functions normalize, not all energies are possible (remember, this is similar to the particle in a box situation / energy quantization).
A quick note about the Bohr model: it is wrong. Electrons do not just go in a 2D circle around the nucleus. It is crazy (lucky) that Bohr actually got the right answer. This is why the Bohr model was so famous. Before people could really comprehend this mathematically, somehow Bohr was telling people the right answers for their experimental results. It had some things to do with luck, but Bohr did use quantization of angular momentum (which back then, like now, was hard for people to think about). So Bohr's model did get some things right (and was very novel to think of). Going back to the Bohr model, Bohr defined a very useful constant: the Bohr radius. We can use this constant below:
It is important to note that we can have further splitting of the energy due to spin magnetism, the Zeeman effect, hyperfine splitting, and relativistic effects, but for slow moving Hydrogen atoms not in a magnetic field, this is the energy.
The last thing to do is to finish solving the wave function of the Hydrogen atom. To begin, let us plug back in our initial definitions from the top of the page:
The last thing to do is to finish solving the wave function of the Hydrogen atom. To begin, let us plug back in our initial definitions from the top of the page:
And that is the brute force way of solving the Hydrogen atom radial equation for some 'n' index. We know that 'n' index's energy states as 'n' is related proportional to energy (so we call n = 1 the first excited state, n = 2 the second excited state, and so on). To be clear, we start the index not at n = 0, but at n = 1 (but you can add +/- 1 to the constant as long as you are internally consistent). For us, since energy is 1/n^2, n can never be zero.
Quantum numbers:
'n': We call 'n' a quantum number as it directly tells us information about an observable (the energy) of the atom
'J': We call 'J' a quantum number as mathematically (although not discussed) it is the number of radial nodes present
'L': We have already introduced 'L,' which tells us about the magnitude of the observable angular momentum.
'm': We have already found the magnetic quantum number 'm' (the z-projection of the angular momentum)
With all of our variables defined (and related to an experimental quantity), we can now solve the radial solution to the Hydrogen atom.
Quantum numbers:
'n': We call 'n' a quantum number as it directly tells us information about an observable (the energy) of the atom
'J': We call 'J' a quantum number as mathematically (although not discussed) it is the number of radial nodes present
'L': We have already introduced 'L,' which tells us about the magnitude of the observable angular momentum.
'm': We have already found the magnetic quantum number 'm' (the z-projection of the angular momentum)
With all of our variables defined (and related to an experimental quantity), we can now solve the radial solution to the Hydrogen atom.
We have now solved the wave function psi of the Hydrogen atom (We found the radial component in this page and the angular component in the last page). Note, for the radial component, inputting an energy will constrain the 'n' quantum number and inputting a specific orbital will constrain the 'L' quantum number. Altogether, knowing 'n' and 'L' constrained the quantum number 'J.' Once this is know, everything else in the radial equation is either a constant or the variable 'r.'
The last steps when actually solving the Hydrogen atom would be to put the angular and radial components together (like in equation 58) and normalize the function over all 3D space.
The last steps when actually solving the Hydrogen atom would be to put the angular and radial components together (like in equation 58) and normalize the function over all 3D space.
|
|
|