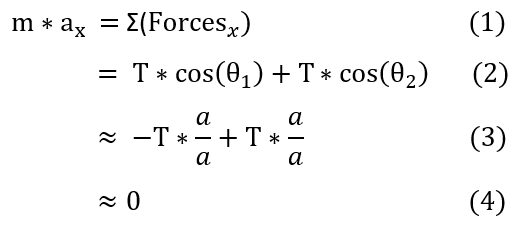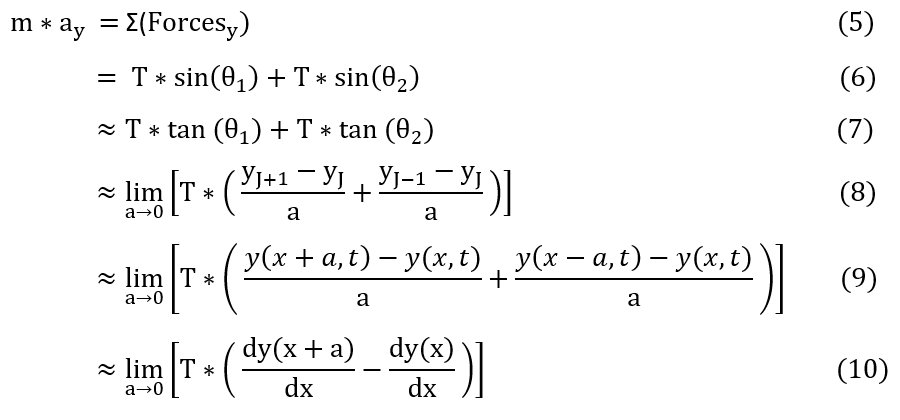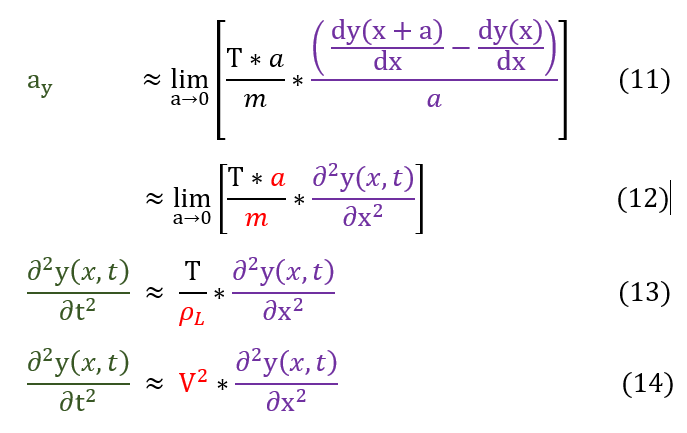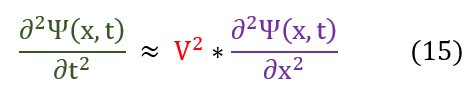Mind Network - Samuel Solomon
Introduction to Waves
The Wave Equation
|
|
|
As we begin our journey into Quantum Mechanics, it is important for us to highlight what exactly someone means when they say the buzzword "wave" (in wave-particle duality, wave function, and wave equation). In order to comprehend these terms, let us start with the simplest 2-D wave model: particles on a string with small oscillations. Mathematically modeling this wave can be difficult. Therefore, before we get bogged down in the math, let us consider some simplifying assumptions about these particles.
1. The distance between any two adjacent particles is very small
Motivation: On a real string, particles are on the order of angstroms apart.
2. The total distance between any two adjacent particles is essentially a constant value called 'a'
Motivation: For small oscillations, the DeltaY does not change significantly enough to change the total distance.
3. The x-displacement (DeltaX) between any two particles is essentially a constant called 'a' (like the total distance)
Motivation: For small oscillations, DeltaY does not change significantly enough to contribute to the total distance.
4. The relevant interactions are from adjacent atoms: called nearest neighbor interactions (first order approximation)
Motivation: The force between two particles decay at a rate of 1/(r^2). Greater distance = less relevance.
5. All particles feel the same magnitude force (The angle changes as the adjacent particle oscillates)
Motivation: Force is a function of distance and the particles are all about the same distance apart.
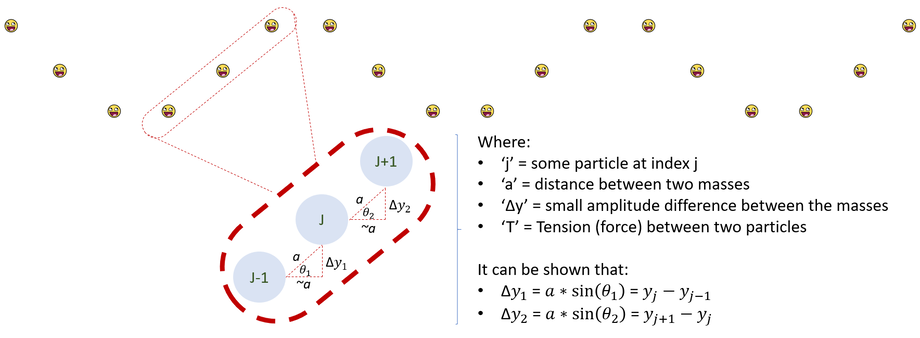
It is important to note that these assumptions may not always be true and only apply for small wave oscillations. We can therefore appreciate that second and third order approximations have been calculated. Nonetheless, to start our wave discussion, we can now use these key (first-order) assumptions to model and mathematically interpret the wave below:
1. The distance between any two adjacent particles is very small
Motivation: On a real string, particles are on the order of angstroms apart.
2. The total distance between any two adjacent particles is essentially a constant value called 'a'
Motivation: For small oscillations, the DeltaY does not change significantly enough to change the total distance.
3. The x-displacement (DeltaX) between any two particles is essentially a constant called 'a' (like the total distance)
Motivation: For small oscillations, DeltaY does not change significantly enough to contribute to the total distance.
4. The relevant interactions are from adjacent atoms: called nearest neighbor interactions (first order approximation)
Motivation: The force between two particles decay at a rate of 1/(r^2). Greater distance = less relevance.
5. All particles feel the same magnitude force (The angle changes as the adjacent particle oscillates)
Motivation: Force is a function of distance and the particles are all about the same distance apart.
It is important to note that these assumptions may not always be true and only apply for small wave oscillations. We can therefore appreciate that second and third order approximations have been calculated. Nonetheless, to start our wave discussion, we can now use these key (first-order) assumptions to model and mathematically interpret the wave below:
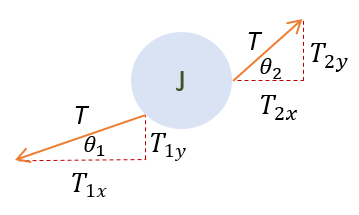
With the picture now defined, it is time to start the physics portion of this problem. At first, this problem may seem daunting as there can be an infinite amount of particles on the string. However, let us tackle this question by looking first at a particle at an arbitrary index (let it be 'j') on the string. Like any good physics problem, we start with newton's second law:
In order to make sure everyone is following, let us review some key steps below:
1 to 2: We add both cosine terms because cosine of theta_1 is a negative quantity already.
2 to 3: We replace both cosine terms with a/a because the x direction is essentially the hypotenuse of the triangle very
small y oscillations (y is approximated to be near zero).
Overall, it seems that the x direction wasn't that helpful. It is time to move onto the y direction.
1 to 2: We add both cosine terms because cosine of theta_1 is a negative quantity already.
2 to 3: We replace both cosine terms with a/a because the x direction is essentially the hypotenuse of the triangle very
small y oscillations (y is approximated to be near zero).
Overall, it seems that the x direction wasn't that helpful. It is time to move onto the y direction.
In order to make sure everyone is following, let us review some key steps below:
6 to 7: We can use the small angle approximation that sin(theta) = theta = tan(theta). This holds as the hypotenuse is
about equal to Delta_x
7 to 8: Tan(theta) = Delta_y/Delta_x. Also, as the particles are super close, we can take the limit as 'a' gets very small.
8 to 9: Taking particle 'j' to be at location x, we can generalize the amplitude / height of any particle to be a function of
y. Where y(x) = y_j.
9 to 10: Taking a closer look at the limit, we can tell that is the definition of a derivative at y(x+a) and y(x).
Let us now divide each side by m*a/a.
6 to 7: We can use the small angle approximation that sin(theta) = theta = tan(theta). This holds as the hypotenuse is
about equal to Delta_x
7 to 8: Tan(theta) = Delta_y/Delta_x. Also, as the particles are super close, we can take the limit as 'a' gets very small.
8 to 9: Taking particle 'j' to be at location x, we can generalize the amplitude / height of any particle to be a function of
y. Where y(x) = y_j.
9 to 10: Taking a closer look at the limit, we can tell that is the definition of a derivative at y(x+a) and y(x).
Let us now divide each side by m*a/a.
In order to make sure everyone is following, let us review some key steps below:
11 to 12: This is the definition of a derivative
12 to 13: Density is defined as mass over volume. Hence, linear mass density (P_L) is defined as mass per unit length.
13 to 14: Sqrt(T/P_L) is experimentally found to be the wave velocity. More tension or smaller mass = higher speed.
In quantum mechanics, we usually refer to the y(x,t) as psi(x,t) as shown below. In either case, it represents the amplitude of a wave. We call the equation below the wave equation.
11 to 12: This is the definition of a derivative
12 to 13: Density is defined as mass over volume. Hence, linear mass density (P_L) is defined as mass per unit length.
13 to 14: Sqrt(T/P_L) is experimentally found to be the wave velocity. More tension or smaller mass = higher speed.
In quantum mechanics, we usually refer to the y(x,t) as psi(x,t) as shown below. In either case, it represents the amplitude of a wave. We call the equation below the wave equation.
|
|
|