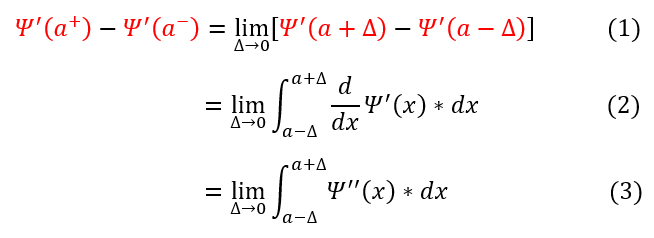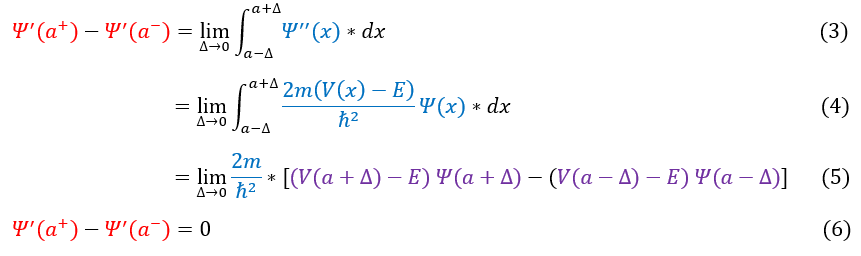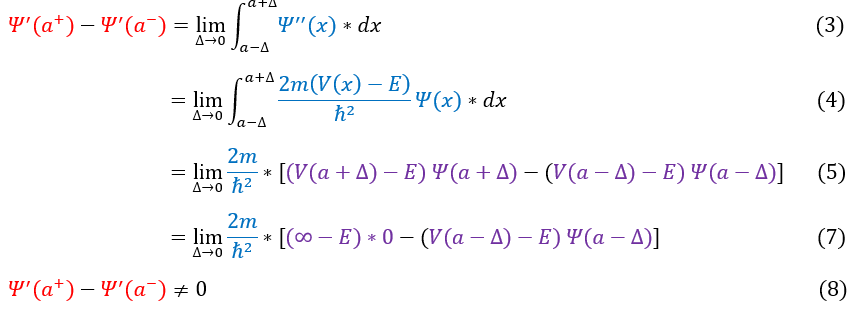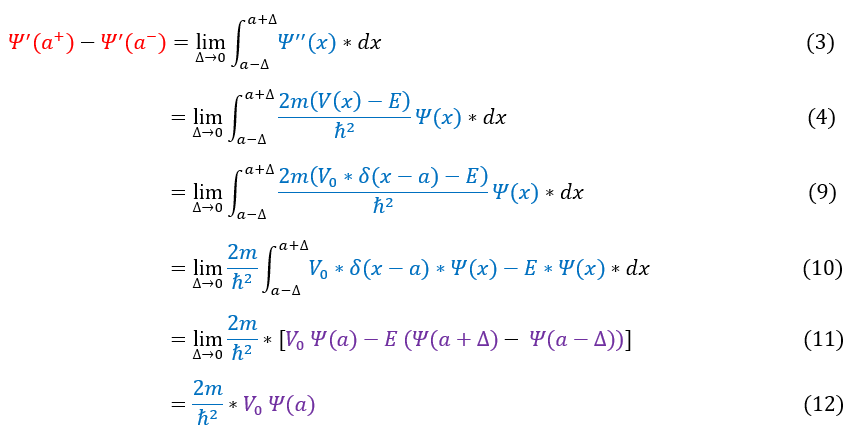Mind Network - Samuel Solomon
Patching Solutions
Finite, Infinite, and Delta Function Potentials
When patching solutions together, two different quantities about the wave function must be considered:
1. The connecting point of the wave function on both sides of the boundary
2. The slope (angle of attack) of the wave function on both sides of the boundary
The wave function, to have real probabilistic interpretations, must be a continuous wave function, so that takes care of the first point. Whether the slope of the wave function has to be continuous is a separate issue that will be discussed in a few cases below.
But first, let us quickly define mathematically what we mean when we ask whether the first derivative (slope) of the wave function is continuous. In order to for the first derivative (the slope) of the wave function to be continuous, we require the difference in the slope of either sides of a boundary (lets say at position 'a') to be zero. Mathematically we can therefore set up this question as:
1. The connecting point of the wave function on both sides of the boundary
2. The slope (angle of attack) of the wave function on both sides of the boundary
The wave function, to have real probabilistic interpretations, must be a continuous wave function, so that takes care of the first point. Whether the slope of the wave function has to be continuous is a separate issue that will be discussed in a few cases below.
But first, let us quickly define mathematically what we mean when we ask whether the first derivative (slope) of the wave function is continuous. In order to for the first derivative (the slope) of the wave function to be continuous, we require the difference in the slope of either sides of a boundary (lets say at position 'a') to be zero. Mathematically we can therefore set up this question as:
We find:
1. If equation 3 equals zero: the slope is continuous
2. If equation 3 is non-zero: the slope is discontinuous
1. If equation 3 equals zero: the slope is continuous
2. If equation 3 is non-zero: the slope is discontinuous
CASE I: V(x) is finite and continuous
In order to make sure everyone is following, let us review some key steps below:
3 to 4: Plug in the time independent Schrodinger equation for the second derivative of the wave function
4 to 5: The integral of a point (which is the case as delta goes to zero) is just the point itself (sum up 1 point)
5 to 6: As the limit of delta goes to zero, we essentially have v*psi - v*psi = 0
This should not shock anyone as the wave function is continuous and finite and the potential is continuous and finite, so it should have a continuous derivative.
3 to 4: Plug in the time independent Schrodinger equation for the second derivative of the wave function
4 to 5: The integral of a point (which is the case as delta goes to zero) is just the point itself (sum up 1 point)
5 to 6: As the limit of delta goes to zero, we essentially have v*psi - v*psi = 0
This should not shock anyone as the wave function is continuous and finite and the potential is continuous and finite, so it should have a continuous derivative.
CASE II: V(x) is an infinite wall (discontinuous)
In order to make sure everyone is following, let us review some key steps below:
3 to 5: The same steps as the first case
5 to 7: V is infinity on one side (which we previously found makes the wave function 0)
7 to 8: Infinity * 0 is very ambiguous. Is it zero, is it still infinity. Either way, the whole equation is definitely not zero.
The slope is is not continuous, and it is ambiguous to what the difference in the slope is.
3 to 5: The same steps as the first case
5 to 7: V is infinity on one side (which we previously found makes the wave function 0)
7 to 8: Infinity * 0 is very ambiguous. Is it zero, is it still infinity. Either way, the whole equation is definitely not zero.
The slope is is not continuous, and it is ambiguous to what the difference in the slope is.
CASE II: V(x) is a Delta Function (discontinuous, infinite point)
In order to make sure everyone is following, let us review some key steps below:
3 to 4: The same steps as the first two cases
4 to 9: Plug in the delta function potential for V(x)
9 to 10: Pull out the constants from the integral
10 to 11: Solve the integral (Note: the delta function is zero in every place except when x = a)
11 to 12: Evaluate the limit
When we have a delta function potential, we still do not have continuous first derivative of the wave function, but we do have a known finite difference that we can calculate.
3 to 4: The same steps as the first two cases
4 to 9: Plug in the delta function potential for V(x)
9 to 10: Pull out the constants from the integral
10 to 11: Solve the integral (Note: the delta function is zero in every place except when x = a)
11 to 12: Evaluate the limit
When we have a delta function potential, we still do not have continuous first derivative of the wave function, but we do have a known finite difference that we can calculate.
SUMMARY OF RESULTS
When we patch together solutions for the wave function we will use the following rules:
1. No matter what: the wave function psi(x) is always continuous and finite
2. If the potential is finite, the slope of the wave function on either side of the boundary is the same.
3. If the potential is infinite, the slope is discontinuous at the boundary (finite difference for delta functions)
1. No matter what: the wave function psi(x) is always continuous and finite
2. If the potential is finite, the slope of the wave function on either side of the boundary is the same.
3. If the potential is infinite, the slope is discontinuous at the boundary (finite difference for delta functions)
|
|
|