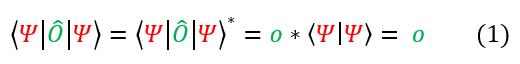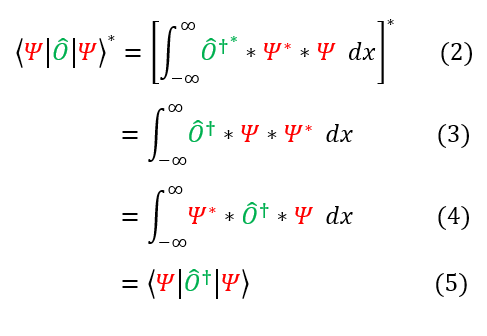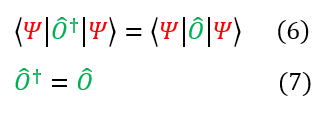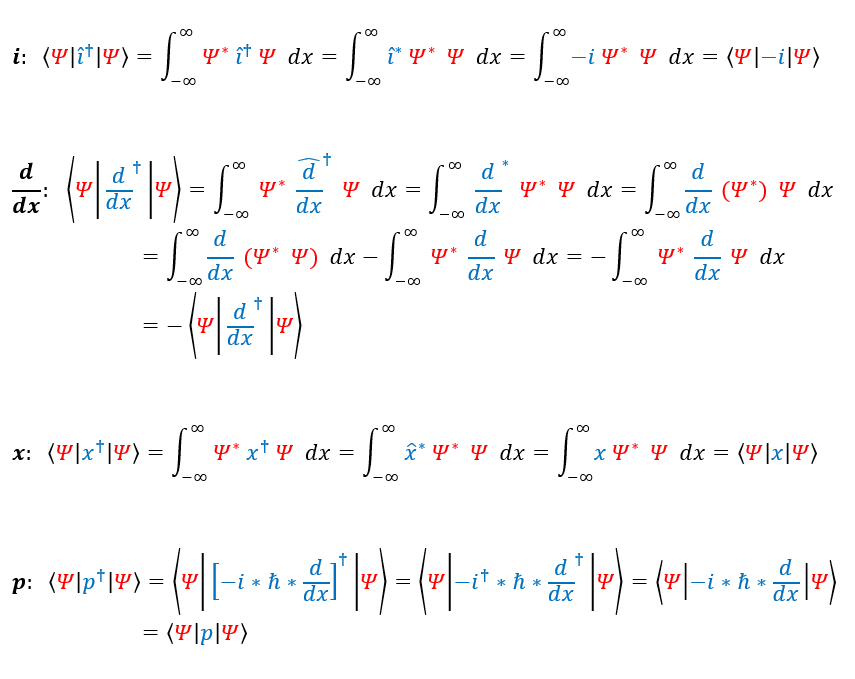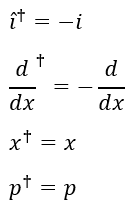Mind Network - Samuel Solomon
Introduction to Quantum Operators
The Hermitian and the Adjoint
After discussing quantum operators, one might start to wonder about all the different operators possible in this world. I claimed that the requirement is only that the wave function is an eigenfuntion of the operator. While this leads to many types of operators, not all of them are experimentally observed. These specific type of operators are called hermitian operators.
Hermitian operators are operators that correspond to eigenvalues that we can physically observe. If we can physically observe the eigenvalue, then the eigenvalue must be real. Hence, hermitian operators are defined as operators that correspond to real eigenvalues. Mathematically this is represented below:
Hermitian operators are operators that correspond to eigenvalues that we can physically observe. If we can physically observe the eigenvalue, then the eigenvalue must be real. Hence, hermitian operators are defined as operators that correspond to real eigenvalues. Mathematically this is represented below:
Note that the complex conjugate of a function is represented with a star (*) above it. In equation 1 we can appreciate that because the eigenvalue is real, the complex conjugate of the real eigenvalue is just the real eigenvalue (no imaginary term to take the complex conjugate of). We can now expand the expression above:
In order to make sure everyone is following, let us review some key steps below:
2: We took the expression from equation 1 and wrote it in integral format
2 to 3: took the complex conjugate of every variable
3 to 4: Rearranged the order of the wave functions into a familiar format
4 to 5: switched back to Dirac notation.
While this expression may not seem so significant at first, we can recall that the inner product (<psi|O|psi>) is equal to its complex conjugate. Hence:
2: We took the expression from equation 1 and wrote it in integral format
2 to 3: took the complex conjugate of every variable
3 to 4: Rearranged the order of the wave functions into a familiar format
4 to 5: switched back to Dirac notation.
While this expression may not seem so significant at first, we can recall that the inner product (<psi|O|psi>) is equal to its complex conjugate. Hence:
This is a non-trivial solution found based on one simple assumption: the eigenvalue is real (and observable). What we have shown is that for any hermitian eigenfunction (real eigenvalue, observable quantity), the operator is equal to its own adjoint. We call these operators self-adjoint.
A summary about hermitian operators is shown below:
1. Hermitian operators are defined to have real observables and real eigenvalues.
2. Hermitian operator's are self-adjoint.
3. Hermitian operators, in matrix format, are diagonalizable.
4. The transpose of the transpose of an operator is just the operator. Hence the adjoint of the adjoint is the operator.
4. If the adjoint of an operator is the negative of the operator, we call these anti-hermitian.
Example: i = sqrt(-1) -> not real. Note that two antihermitian operators can combine to make a hermitian operator
Operators that are hermitian (observable) include the position, momentum, and energy. Here are a list of common adjoint operators:
A summary about hermitian operators is shown below:
1. Hermitian operators are defined to have real observables and real eigenvalues.
2. Hermitian operator's are self-adjoint.
3. Hermitian operators, in matrix format, are diagonalizable.
4. The transpose of the transpose of an operator is just the operator. Hence the adjoint of the adjoint is the operator.
4. If the adjoint of an operator is the negative of the operator, we call these anti-hermitian.
Example: i = sqrt(-1) -> not real. Note that two antihermitian operators can combine to make a hermitian operator
Operators that are hermitian (observable) include the position, momentum, and energy. Here are a list of common adjoint operators:
There are two ways of finding an adjoint of an operator. You could either start with the Dirac notation and get from the adjoint of the operator to a function without any adjoints, or you could break the operator up into smaller pieces and take the adjoint of all the pieces individually.
I tried to show the method for a few common examples above, but let us quickly talk about the math used for each case:
i: I start from the adjoint operator of i (sqrt(-1)). When I act on the function to the left, I take the adjoint and complex
conjugate of i. Th adjoint of the adjoint returns my intiial operator and the complex conjugate of i is -i. Hence the
adjoint of i is just -i (anti-hermitian).
d/dx: I start the exact same way as I do for "i", but now d/dx is a real function. The difference is that "i" is a scalar and
can commute with any function like psi, while d/dx cannot. The first step is to use integration by part, which takes the form integral (d/dx*(f*g) )=integral( (d/dx(f) * g + f * d/dx (g). Next, we realize that the integral of the
derivative of |psi|^2 is just zero because |psi|^2 decays at +/- infinity to zero.
x: The x operator on psi = x, which is a real value; hence the complex conjugate does nothing to it.
p: We can replace p with its functional form and notice that we already solved for their adjoint in the above.
For completeness, here are the adjoint of these operators listed neatly below:
I tried to show the method for a few common examples above, but let us quickly talk about the math used for each case:
i: I start from the adjoint operator of i (sqrt(-1)). When I act on the function to the left, I take the adjoint and complex
conjugate of i. Th adjoint of the adjoint returns my intiial operator and the complex conjugate of i is -i. Hence the
adjoint of i is just -i (anti-hermitian).
d/dx: I start the exact same way as I do for "i", but now d/dx is a real function. The difference is that "i" is a scalar and
can commute with any function like psi, while d/dx cannot. The first step is to use integration by part, which takes the form integral (d/dx*(f*g) )=integral( (d/dx(f) * g + f * d/dx (g). Next, we realize that the integral of the
derivative of |psi|^2 is just zero because |psi|^2 decays at +/- infinity to zero.
x: The x operator on psi = x, which is a real value; hence the complex conjugate does nothing to it.
p: We can replace p with its functional form and notice that we already solved for their adjoint in the above.
For completeness, here are the adjoint of these operators listed neatly below:
|
|
|