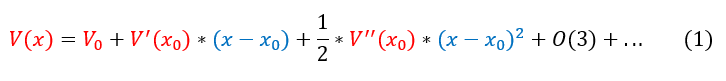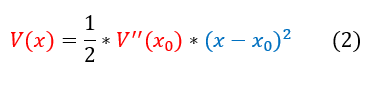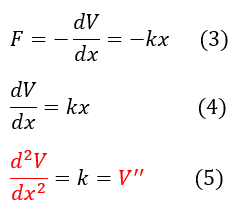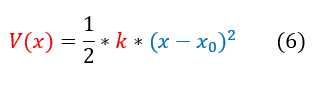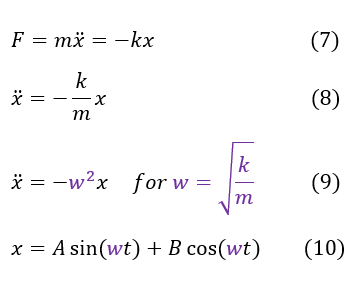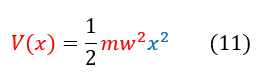Mind Network - Samuel Solomon
Quantum Harmonic Oscillator
Classical Mechanics Analogue
In classical mechanics we define a harmonic oscillator as a system that experiences a restoring force when perturbed away from equilibrium. Classical examples include:
1. Spring: when displaced from the natural length, the spring either pushes or pulls the system back to equilibrium
2. Pendulum: When displaced from the natural hanging position, gravity pulls the system back down to equilibrium
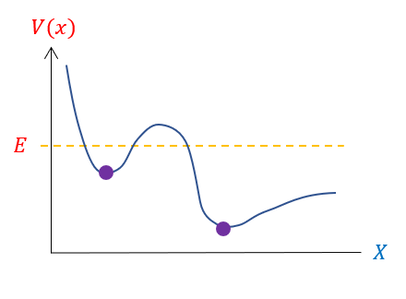
Nature finds this equilibrium position to be the most stable form of the system. It is found to be the local minimum on potential energy diagram:
1. Spring: when displaced from the natural length, the spring either pushes or pulls the system back to equilibrium
2. Pendulum: When displaced from the natural hanging position, gravity pulls the system back down to equilibrium
Nature finds this equilibrium position to be the most stable form of the system. It is found to be the local minimum on potential energy diagram:
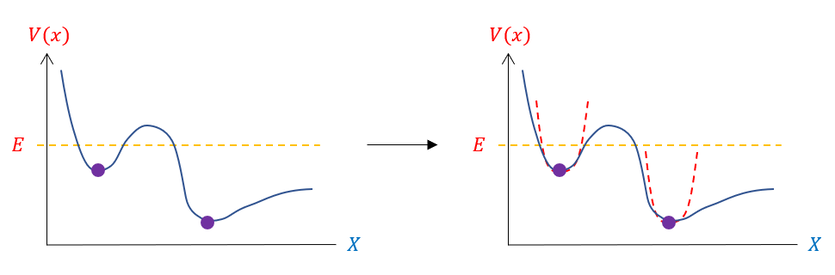
The purple dots in the picture above represent points that exhibit this restorative force. If the particle moves to the left or to the right of the purple dot, the particle faces a greater energy barrier and is pulled back down ("falls back down") to reach its local minimum energy state again.
Depending on one's familiarity with harmonic oscillators, one might start to be correctly questioning how one system can approximate different energy minimums (the two local minimums in the diagram above are obviously NOT the same). To address this question, we must quickly note that harmonic oscillators APPROXIMATE the local minimum for SMALL oscillations. In fact, the mathematical representation for harmonic oscillators clearly show this assumption, which is actually why the harmonic oscillators approximation can only be used for local minimum that show this characteristic concave up parabola (though applications to local maximum, concave down parabolas, are possible).
The mathematical way of approximating functions is to Taylor expand around a point. Let us Taylor expand around one of the local minimum points 'x' that has a corresponding potential energy value of 'V_0'
Depending on one's familiarity with harmonic oscillators, one might start to be correctly questioning how one system can approximate different energy minimums (the two local minimums in the diagram above are obviously NOT the same). To address this question, we must quickly note that harmonic oscillators APPROXIMATE the local minimum for SMALL oscillations. In fact, the mathematical representation for harmonic oscillators clearly show this assumption, which is actually why the harmonic oscillators approximation can only be used for local minimum that show this characteristic concave up parabola (though applications to local maximum, concave down parabolas, are possible).
The mathematical way of approximating functions is to Taylor expand around a point. Let us Taylor expand around one of the local minimum points 'x' that has a corresponding potential energy value of 'V_0'
While the whole Taylor expansion to the infinity term will give us exactly the whole function, we only care about small oscillations around the local minimum. Hence, we will make a few approximations:
1. For a small X-X_0 perturbation, ( X-X_0 )^3 or higher (order three terms) will essentially be zero
Think about (0.01)^3 vs. (0.01)^2. Both may be small, but (0.01)^3 is much smaller (less experimentally relevant)
2. Because we are always around a local minimum, the first derivative of the potential is zero
For small perturbations, the first derivative does not change much (still zero). Force = - dV/dx = 0 at equilibrium
3. We can set the reference potential to be V_0 = 0
A potential without a reference is meaningless (V = mgh is really ΔV= mg*Δh). The reference is arbitrary
We can now approximate the potential for small perturbations (for small oscillations) as:
1. For a small X-X_0 perturbation, ( X-X_0 )^3 or higher (order three terms) will essentially be zero
Think about (0.01)^3 vs. (0.01)^2. Both may be small, but (0.01)^3 is much smaller (less experimentally relevant)
2. Because we are always around a local minimum, the first derivative of the potential is zero
For small perturbations, the first derivative does not change much (still zero). Force = - dV/dx = 0 at equilibrium
3. We can set the reference potential to be V_0 = 0
A potential without a reference is meaningless (V = mgh is really ΔV= mg*Δh). The reference is arbitrary
We can now approximate the potential for small perturbations (for small oscillations) as:
The next obvious question is what is the second derivative of the potential around the local minimum. To answer this question, let us apply the harmonic oscillator to a problem. In quantum mechanics we will generally represent electrostatic forces as springs osculating, so let us use a spring as an example. The restorative force on a spring is F = -kx. We also know that F = - dV/dx in one dimension (it is the gradient for 3 dimensions). Let us combine these two facts below:
Hence the potential energy of a spring is:
Except knowing the 'k' constant (the force constant) between atoms is not always a trivial matter. However, we can experimentally find the frequency of oscillation. We can find 'k' in terms of the frequency 'w' below:
In order to make sure everyone is following, let us review some key steps below:
7: Newton's second law. The sum of all forces = mass*acceleration
7 to 8: divide both sides by 'm'
8 to 9: set w^2 = k/m
9 to 10: solve the differential equation and notice that 'w' is the oscillation frequency
Replacing 'k' for 'w' in the harmonic oscillator potential will give us our final general harmonic oscillator form:
7: Newton's second law. The sum of all forces = mass*acceleration
7 to 8: divide both sides by 'm'
8 to 9: set w^2 = k/m
9 to 10: solve the differential equation and notice that 'w' is the oscillation frequency
Replacing 'k' for 'w' in the harmonic oscillator potential will give us our final general harmonic oscillator form:
This V(x) potential holds for any small oscillation around a local minimum potential with variables defined as:
m = mass of the particle
w = oscillation frequency of the particle in radians / second (pronounced 'omega')
x = the displacement from the equilibrium x coordinate (used to be x - x_0 where 'x' was the equilibrium position)
A last final word about the harmonic oscillator is a warning. Harmonic oscillators only describe small oscillations. A pictorial representation of the harmonic oscillator's fit to a local minimum can be seen below:
m = mass of the particle
w = oscillation frequency of the particle in radians / second (pronounced 'omega')
x = the displacement from the equilibrium x coordinate (used to be x - x_0 where 'x' was the equilibrium position)
A last final word about the harmonic oscillator is a warning. Harmonic oscillators only describe small oscillations. A pictorial representation of the harmonic oscillator's fit to a local minimum can be seen below:
To fit the curve better, we can only change the width of the parabola. For the same particle (same mass) the only free parameter is the frequency of oscillation. Higher frequency would mean a smaller width parabola; lower frequency would mean a higher width of the parabola.
|
|
|