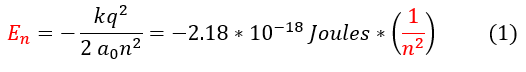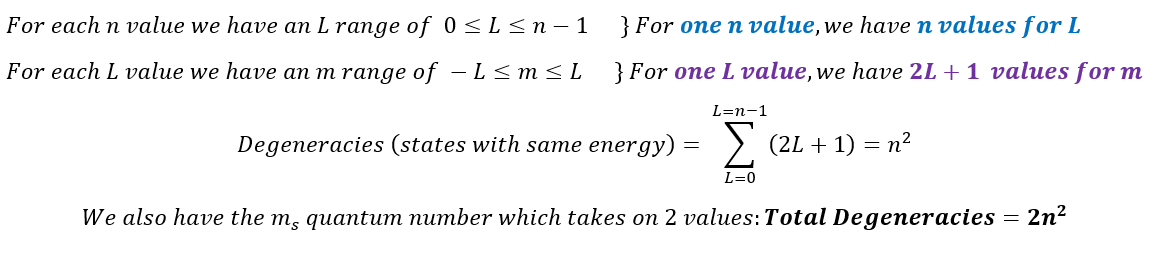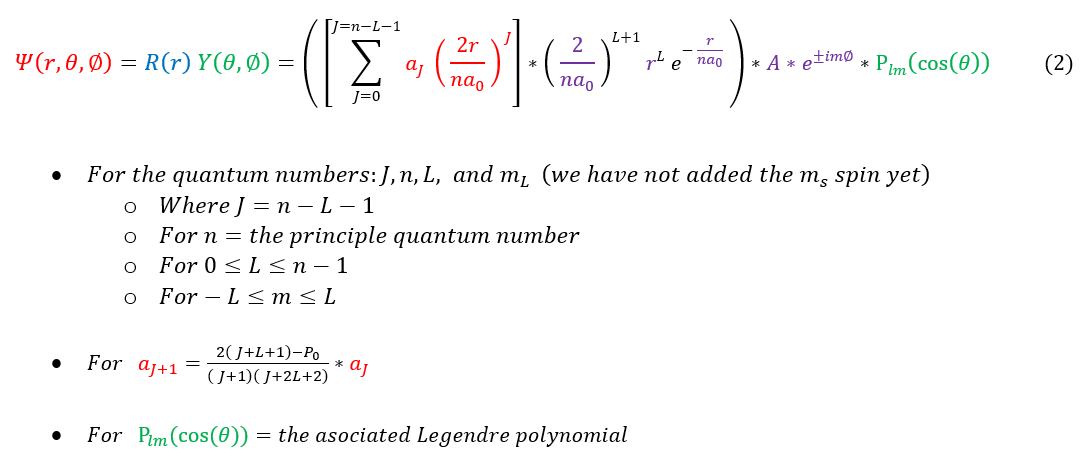Mind Network - Samuel Solomon
Hydrogen Atom
Recap
|
|
|
Congratulations, you have now finished the Mind Network: Quantum mechanics I course. Throughout the course, you have been trained to think and solve problems from a quantum mechanical framework, throwing out your classical mechanic's intuition for the first principle understanding of small particles. Using well defined postulates, we were able to take our generalized 1-dimensional problems to work our way up to the Hydrogen atom solution.
For the last page of this course, let us just quickly recap (conglomerate the information of) what we have found for the Hydrogen atom. We will start with the energy:
For the last page of this course, let us just quickly recap (conglomerate the information of) what we have found for the Hydrogen atom. We will start with the energy:
The energy of the Hydrogen atom was first mathematically discovered by Niels Bohr through an incorrect (yet novel at the time) atomic model and quantization of angular momentum. It was extremely ground breaking as it confirmed the strange experimental results (the energy quantization) scientists were getting. We were able to confirm this equation using Quantum mechanics.
For a little history, the energy of the hydrogen atom, as well as other molecules, were experimentally observed as spectral lines (only certain energies were absorbed and emitted). Physicists had to somehow explain this weird phenomenon known as 'quantization of energy.' There were certain observables in the universe that could, for some reason, NEVER take on certain values. This was hard to grasp at the time as we can classically generate objects with what, at least for us, seems like any value we want. However, now using quantum mechanics, we mathematically understand that this quantization constraint arises from the need to normalize the wave function (a particle taking on a certain value is probabilistic and therefore we must have a finite amount of possibilities).
Another note about energy is that, in 1-dimension, we found that a quantum system cannot have degenerate states (multiple energies for one state). However, we are allowed to have degenerate states in 3-dimensions. In fact, we can see this for Hydrogen. The energy of an electron in Hydrogen depends on its 'n' quantum number. Therefore:
For a little history, the energy of the hydrogen atom, as well as other molecules, were experimentally observed as spectral lines (only certain energies were absorbed and emitted). Physicists had to somehow explain this weird phenomenon known as 'quantization of energy.' There were certain observables in the universe that could, for some reason, NEVER take on certain values. This was hard to grasp at the time as we can classically generate objects with what, at least for us, seems like any value we want. However, now using quantum mechanics, we mathematically understand that this quantization constraint arises from the need to normalize the wave function (a particle taking on a certain value is probabilistic and therefore we must have a finite amount of possibilities).
Another note about energy is that, in 1-dimension, we found that a quantum system cannot have degenerate states (multiple energies for one state). However, we are allowed to have degenerate states in 3-dimensions. In fact, we can see this for Hydrogen. The energy of an electron in Hydrogen depends on its 'n' quantum number. Therefore:
Note: we haven't actually gone over the m_s quantum number in much detail yet. For reference, it is the spin quantum number (which has two values for an electron: +/- 1/2). We will go over spin more in the next course: Quantum Mechanics II.
To be clear, our 4-quantum numbers (with their common names) are listed as follows:
n = the principle quantum number. Tells us about the energy of the atom. Listed as the row # on the periodic table.
While not mathematically related, it does scale with the atomic radius.
L = the angular momentum quantum number. Takes any value from 0 to n - 1. Tells us about the angular momentum of
the atom. The angular momentum distinguishes different orbitals, so L also distinguishes between them.
m_L = the magnetic quantum number. Takes any value from -L to L. Experimentally seen in the Stern-Gerlach
experiment. Physically tells us about the z-component (and hence orientation) of the angular momentum.
m_s = the spin quantum number. Takes on the values of +/- 1/2 for an electron, though we can have particles with
greater spin
The Pauli exclusion principle tells us that no 2 electrons can have the same quantum numbers in the same atom. We call particles that follow this rule Fermions (which includes leptons: electrons). We call particles that break this rule Bosons.
The last quantum number sometimes (as it is obvious from knowing the others) discussed is:
J = the radial quantum number. Not part of the 4 core reported ones as J = n - L - 1 (and hence is deduced from
knowing the others). Experimentally, it has been shown to give us information about the radial nodes in the atom.
The last piece of the puzzle to report is the FULL wave function of the Hydrogen atom (not including the spin). The full wave function we have found for the Hydrogen atom is:
To be clear, our 4-quantum numbers (with their common names) are listed as follows:
n = the principle quantum number. Tells us about the energy of the atom. Listed as the row # on the periodic table.
While not mathematically related, it does scale with the atomic radius.
L = the angular momentum quantum number. Takes any value from 0 to n - 1. Tells us about the angular momentum of
the atom. The angular momentum distinguishes different orbitals, so L also distinguishes between them.
m_L = the magnetic quantum number. Takes any value from -L to L. Experimentally seen in the Stern-Gerlach
experiment. Physically tells us about the z-component (and hence orientation) of the angular momentum.
m_s = the spin quantum number. Takes on the values of +/- 1/2 for an electron, though we can have particles with
greater spin
The Pauli exclusion principle tells us that no 2 electrons can have the same quantum numbers in the same atom. We call particles that follow this rule Fermions (which includes leptons: electrons). We call particles that break this rule Bosons.
The last quantum number sometimes (as it is obvious from knowing the others) discussed is:
J = the radial quantum number. Not part of the 4 core reported ones as J = n - L - 1 (and hence is deduced from
knowing the others). Experimentally, it has been shown to give us information about the radial nodes in the atom.
The last piece of the puzzle to report is the FULL wave function of the Hydrogen atom (not including the spin). The full wave function we have found for the Hydrogen atom is:
For reference, the first few spherical harmonics Y(theta, phi), which is a function of the quantum numbers L and m, are shown below (I am reporting the ones most commonly used):
|
|
|