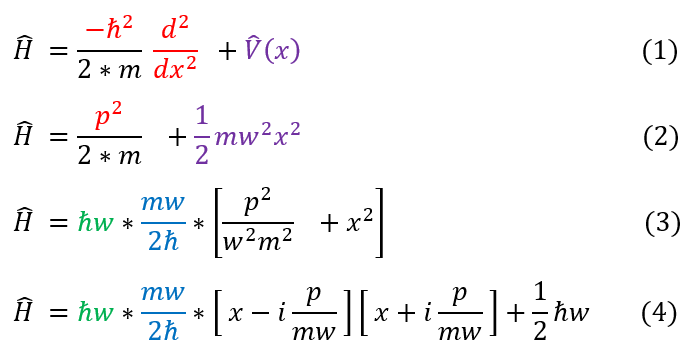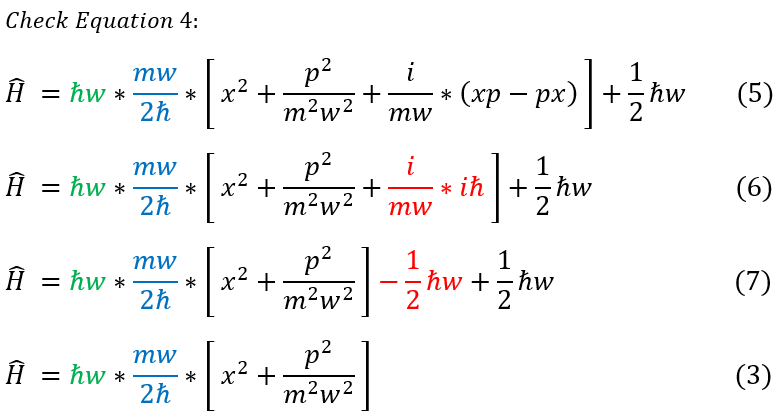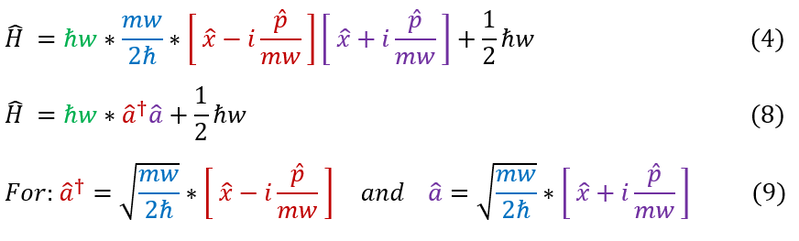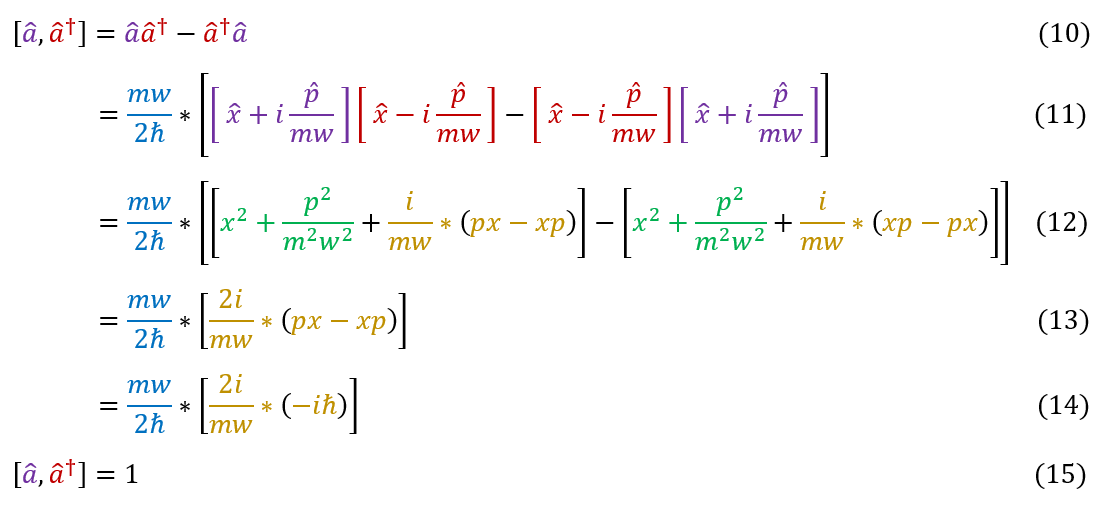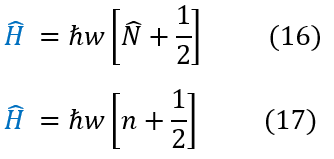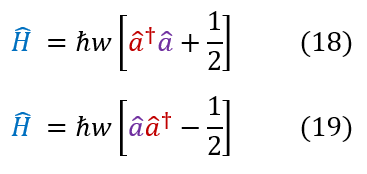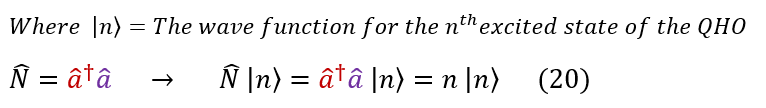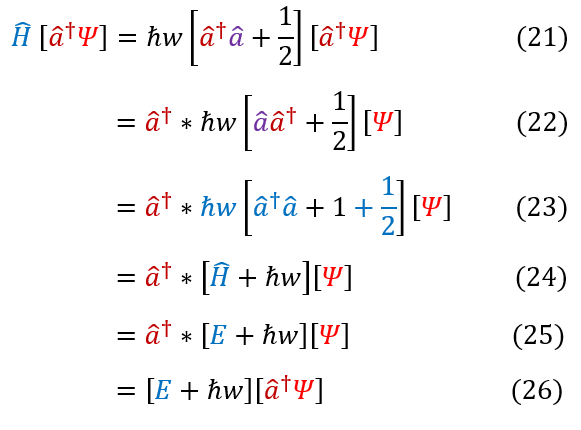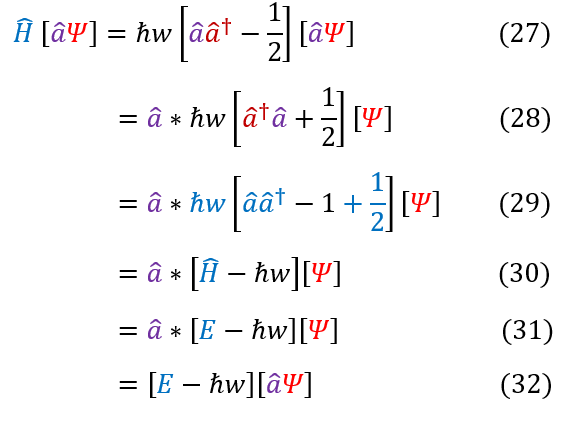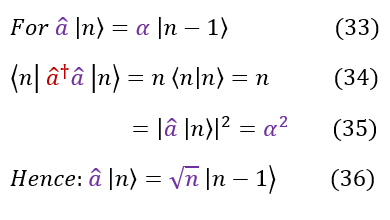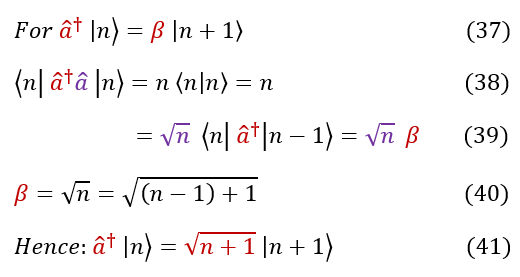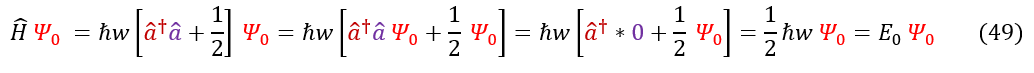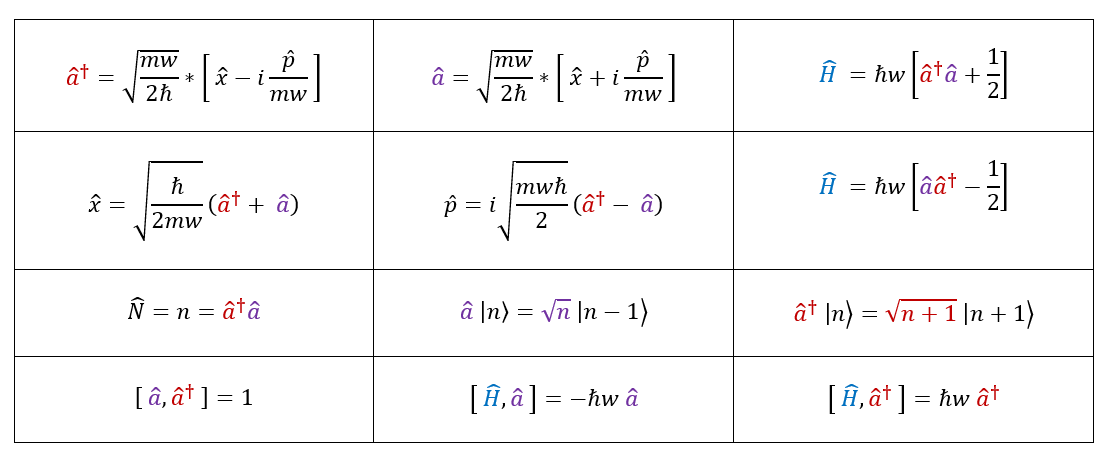Mind Network - Samuel Solomon
Quantum Harmonic Oscillator
Ladder Operators
|
|
|
There is a more elegant way of dealing with Quantum Harmonic Oscillators than the horrible math that occurred on the last page. For perspective, the brute force method of solving quantum harmonic oscillators predated ladder operators, which is why it is important to see that perspective first. Ladder operators, like any other physics operator, has no mathematical motivation and is purely defined to act on some eigenvector to produce some observable eigenvalue. With this is mind, let us rearrange the Schrödinger equation and pull out functions that we will for now call the ladder operators (and later in the page show their mathematical significance):
In order to make sure everyone is following, let us review some key steps below:
1: The Hamiltonian expression
1 to 2: Write the Hamiltonian in terms of p^2 (p= - i h_bar d/dx) and plug in the harmonic potential (x^2 term)
2 to 3: Factor out some constants to get an expression similar to a^2+b^2 (easy to factor)
3 to 4: Factorize the p^2 and x^2 terms; however, xp does not equal px (end up with an extra term)
In case steps 3 to 4 is confusing, a quick check is done on the right:
5: Just Equation 4, but each term distributed out
5 to 6: xp - px = [x,p] = i h_bar
6 to 7: Pull out the red constant
7 to 3: Cancel out the red constant and realize that it is indeed the same as equation 3
We are now in the correct format to define our ladder operators (which are for now just mathematical functions):
1: The Hamiltonian expression
1 to 2: Write the Hamiltonian in terms of p^2 (p= - i h_bar d/dx) and plug in the harmonic potential (x^2 term)
2 to 3: Factor out some constants to get an expression similar to a^2+b^2 (easy to factor)
3 to 4: Factorize the p^2 and x^2 terms; however, xp does not equal px (end up with an extra term)
In case steps 3 to 4 is confusing, a quick check is done on the right:
5: Just Equation 4, but each term distributed out
5 to 6: xp - px = [x,p] = i h_bar
6 to 7: Pull out the red constant
7 to 3: Cancel out the red constant and realize that it is indeed the same as equation 3
We are now in the correct format to define our ladder operators (which are for now just mathematical functions):
Equation 9 has the two functions which we will now on call ladder operators. The red 'a_dagger' is called the raising operator and the purple 'a' is called the lowering operator. A quick visual note about the operators is that the raising and lowering operators are complex conjugates of each other (they are actually the adjoint to each other). Since the operators are not equal to their own adjoint, they are not hermitian and do not correspond to physical observables. To understand their significance, let us first understand their properties. The first one to analyze is the commutator:
In order to make sure everyone is following, let us review some key steps below:
10: The definition of the commutator
10 to 11: Plug in the expressions for the ladder operators
11 to 12: Distribute the functions
12 to 13: The green parts cancel and the yellow parts are the same
13 to 14: The commutator [p,x] = px - xp = - i * h_bar
14 to 15: Simplify the expression
We can now rewrite the Hamiltonian for the quantum harmonic oscillator in four different ways:
10: The definition of the commutator
10 to 11: Plug in the expressions for the ladder operators
11 to 12: Distribute the functions
12 to 13: The green parts cancel and the yellow parts are the same
13 to 14: The commutator [p,x] = px - xp = - i * h_bar
14 to 15: Simplify the expression
We can now rewrite the Hamiltonian for the quantum harmonic oscillator in four different ways:
In order to make sure everyone is following, let us review some key steps below:
16 and 17: The QHO energy equation we derived on the last page. 'N' is the number operator with eigenvalue 'n'
18: How we found to express the Hamiltonian with ladder operators
18 to 19: If you switch the ladder operators, you apply the commutator in equation 15
This is the first time we are introducing the number operator 'N.' It is just an operator that when applied to the quantum harmonic oscillators wave functions, gives back the integer 'n' for the nth excited state. Equations 16 and 17 are really saying the same thing but one is in the eigenvalue form we are used to and one is in the operator form. By comparison to equation 18, we know what the number operator is: it is just the 'a_dagger' * 'a' operator. To visualize this, let us explicitly say this below (note that we are using Dirac notation below):
16 and 17: The QHO energy equation we derived on the last page. 'N' is the number operator with eigenvalue 'n'
18: How we found to express the Hamiltonian with ladder operators
18 to 19: If you switch the ladder operators, you apply the commutator in equation 15
This is the first time we are introducing the number operator 'N.' It is just an operator that when applied to the quantum harmonic oscillators wave functions, gives back the integer 'n' for the nth excited state. Equations 16 and 17 are really saying the same thing but one is in the eigenvalue form we are used to and one is in the operator form. By comparison to equation 18, we know what the number operator is: it is just the 'a_dagger' * 'a' operator. To visualize this, let us explicitly say this below (note that we are using Dirac notation below):
Let us now analyze how ladder operators effect the wave function:
In order to make sure everyone is following, let us review some key steps below:
21: The Hamiltonian applied to the function: 'a_dagger' * QHO wave function. Should equal the energy of the function
21 to 22: Pull out an 'a_dagger'
22 to 23: Apply the commutator ['a','a_dagger'] = 1 to switch the two operators
23 to 24: Notice that the blue part is just the Hamiltonian operator
25 to 26: The Hamiltonian acting directly on the wave function is just the energy of that wave function (scales it)
Equations 27 - 32 follows the exact same logic, but now with the 'a' operator
The significance of equations 26 and 32 is that we know exactly which energies correspond to which excited state of the harmonic oscillator. For a QHO wave function psi with energy E, adding h_bar * w excites the state up one and subtracting h_bar * w lowers the state by one. Therefore, it follows, that acting on the wave function by the ladder operators either lowers or raises the excited state of the wave function. In response, we will now call the 'a_dagger' operator the raising operator or creation operator and the 'a' operator the lowering operator or annihilation operator. All of this follows because the energy spectrum for the QHO follows a ladder pattern with each new energy eigenstate differing by exactly h_bar * w.
The last important property about ladder operators its eigenvalue. While it is already clear from equations 26 and 32 that ladder operators do NOT scale QHO wave functions (in fact it changes the QHO wave function to another QHO wave function). Nevertheless, an important question is how much does it scale the new QHO wave function by (for normalization purposes this is very important). Given that we only know what scalar quantity related to ladder operators (the number operator) we will use this to find the eigenvalues of the ladder operators:
21: The Hamiltonian applied to the function: 'a_dagger' * QHO wave function. Should equal the energy of the function
21 to 22: Pull out an 'a_dagger'
22 to 23: Apply the commutator ['a','a_dagger'] = 1 to switch the two operators
23 to 24: Notice that the blue part is just the Hamiltonian operator
25 to 26: The Hamiltonian acting directly on the wave function is just the energy of that wave function (scales it)
Equations 27 - 32 follows the exact same logic, but now with the 'a' operator
The significance of equations 26 and 32 is that we know exactly which energies correspond to which excited state of the harmonic oscillator. For a QHO wave function psi with energy E, adding h_bar * w excites the state up one and subtracting h_bar * w lowers the state by one. Therefore, it follows, that acting on the wave function by the ladder operators either lowers or raises the excited state of the wave function. In response, we will now call the 'a_dagger' operator the raising operator or creation operator and the 'a' operator the lowering operator or annihilation operator. All of this follows because the energy spectrum for the QHO follows a ladder pattern with each new energy eigenstate differing by exactly h_bar * w.
The last important property about ladder operators its eigenvalue. While it is already clear from equations 26 and 32 that ladder operators do NOT scale QHO wave functions (in fact it changes the QHO wave function to another QHO wave function). Nevertheless, an important question is how much does it scale the new QHO wave function by (for normalization purposes this is very important). Given that we only know what scalar quantity related to ladder operators (the number operator) we will use this to find the eigenvalues of the ladder operators:
In order to make sure everyone is following, let us review some key steps below:
33 and 37: The eigenvalue equation. We are looking for the constant 'alpha' and 'beta' for some QHO state |n>
34 and 38: The number operator acting on the normalized QHO state |n>. The constant 'n' goes out of the integral
35: Since 'a_dagger' is just the complex conjugate (adjoint) of 'a': The Bra <n| 'a_dagger' = the ket 'a' |n>
36: Comparing equations 34 and 35, we can cearly see that the eigenvalue alpha is just sqrt(n)
39: Plug in the eigenvalue found for the lowering operator and the 'beta' eigenvalue we are looking for
40: Comparing 38 and 39, clearly beta = sqrt(n), but note that 'a_dagger' acted on |n - 1> NOT |n>
41: Applying what we found in equation 40, we can clearly see that the raising operator has an eigenvalue of sqrt(n+1)
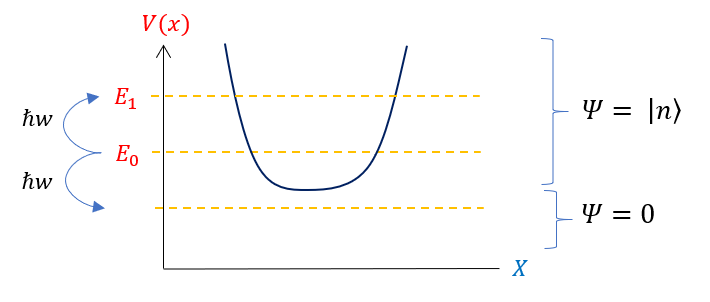
Using ladder operators we can now solve for the ground state wave function of the quantum harmonic oscillator. We can find the ground state by using the fact that it is, by definition, the lowest energy state. So low, that under the ground state is the potential barrier (where the classically disallowed region lies). Since a wave function cannot fully exist in a classically disallowed region, without ever being in a classically allowed region, the wave function must be zero when lowered from the ground state. We can pictorially see this below:
33 and 37: The eigenvalue equation. We are looking for the constant 'alpha' and 'beta' for some QHO state |n>
34 and 38: The number operator acting on the normalized QHO state |n>. The constant 'n' goes out of the integral
35: Since 'a_dagger' is just the complex conjugate (adjoint) of 'a': The Bra <n| 'a_dagger' = the ket 'a' |n>
36: Comparing equations 34 and 35, we can cearly see that the eigenvalue alpha is just sqrt(n)
39: Plug in the eigenvalue found for the lowering operator and the 'beta' eigenvalue we are looking for
40: Comparing 38 and 39, clearly beta = sqrt(n), but note that 'a_dagger' acted on |n - 1> NOT |n>
41: Applying what we found in equation 40, we can clearly see that the raising operator has an eigenvalue of sqrt(n+1)
Using ladder operators we can now solve for the ground state wave function of the quantum harmonic oscillator. We can find the ground state by using the fact that it is, by definition, the lowest energy state. So low, that under the ground state is the potential barrier (where the classically disallowed region lies). Since a wave function cannot fully exist in a classically disallowed region, without ever being in a classically allowed region, the wave function must be zero when lowered from the ground state. We can pictorially see this below:
We can not exists below the QHO potential as the region is classically forbidden and we exponential decay to zero at every point (so the wave function is just zero throughout; there was never a wave function to tunnel anywhere). The annihilation (also called lowering) operator, which is just a mathematical function which we can extract real information from, must also account for this fact. The lowering operator applied to the ground state QHO wave function must annihilate the wave function (kill it; have an eigenvalue of zero). This would only ever happen for a certain function (obvious not all functions will be annihilated when acted upon). We can represent this (and find the ground state eigenfunction using this fact) below:
In order to make sure everyone is following, let us review some key steps below:
42: Lowering operator applied to the ground state wave function
42 to 43: Divide out the blue constant, subtract x * psi, multiply the 'p' term by i/i
43 to 44: Replace the momentum and position operators with their respective eigenvalues
44 to 45: Move the constant over, multiply by psi_0 and integrate the derivative
45 to 46: Integrate both sides
46 to 47: Take both sides and put it in the exponent of 'e'
47 to 48: Simplify the expression using a new constant 'A'
Equation 48 exactly matches our long and mathy proof of the ground state wave function (except we used a dummy variable 'y'). We can also check that the ground state energy matches below:
42: Lowering operator applied to the ground state wave function
42 to 43: Divide out the blue constant, subtract x * psi, multiply the 'p' term by i/i
43 to 44: Replace the momentum and position operators with their respective eigenvalues
44 to 45: Move the constant over, multiply by psi_0 and integrate the derivative
45 to 46: Integrate both sides
46 to 47: Take both sides and put it in the exponent of 'e'
47 to 48: Simplify the expression using a new constant 'A'
Equation 48 exactly matches our long and mathy proof of the ground state wave function (except we used a dummy variable 'y'). We can also check that the ground state energy matches below:
Luckily for us, everything seems consistent with the proof on the last page. Overall, ladder operators have many applications in quantum physics (because we use QHO approximations a lot). While most of the relationships are tedious to show, I wanted to compile the most useful relationships I have found for ladder operators below (not all are proven on this page, but all the math to prove them is here; it is a good exercise for yourself to prove them though):
|
|
|