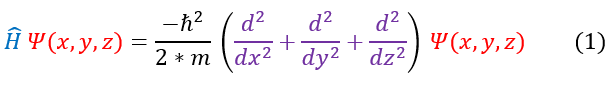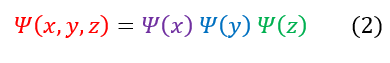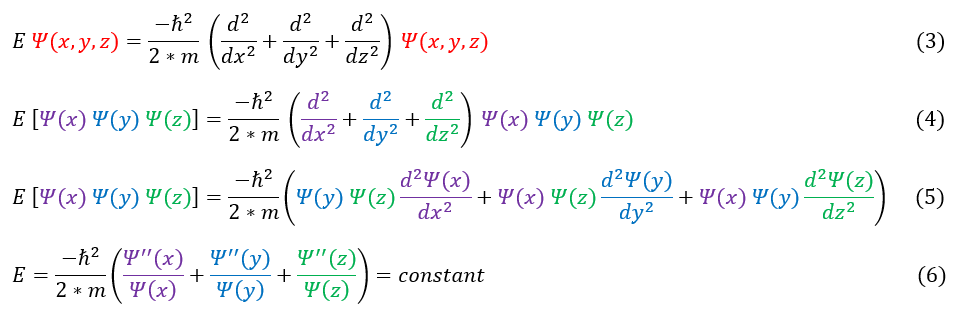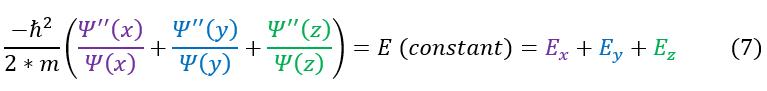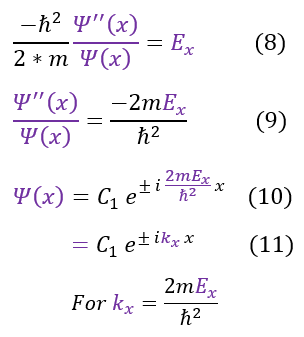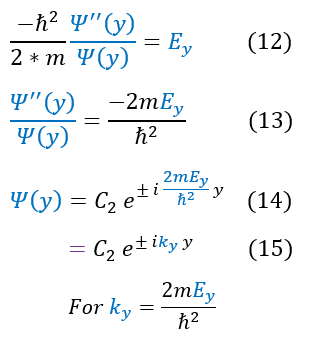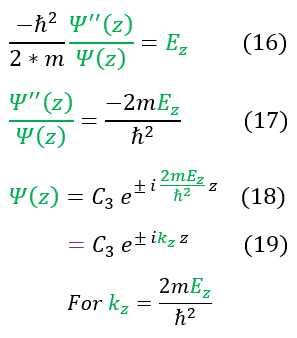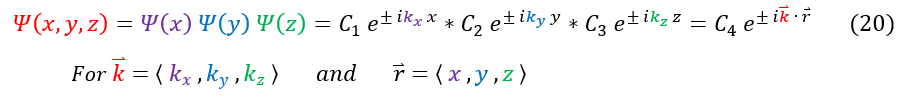Mind Network - Samuel Solomon
Free Particle
|
|
|
Now that we have redefined our Schrödinger equation in 3 dimensions, let us see how this effects the free particle problem we solved earlier. For a quick refresher, a free particle is a particle in a complete vacuum with no external forces acting on it. It is therefore defined to experience no potential barriers (V(x) = 0). The 3 dimensional Schrödinger equation reduces to:
The equation above has 3 different differential equations all in 1 line. This is a little sketchy to solve on its own. We previously made a standing wave approximation for this system (time and position separable) and will in fact use this same principle again to make the equation easier to solve. I know that coordinate systems are man-made mathematical systems used to describe the world. The universe did not feed us this math; therefore, there should be no coordinate preference for a system. In other words, we should not have any preferential probability to be more in the x, y, or z position (they are independent of each other just like time and space). We will therefore make the ansatz that x, y, and z are separable as such:
We are now in a position to solve the Schrödinger equation in equation 1:Schrödinger
In order to make sure everyone is following, let us review some key steps below:
3: The 3-dimensional Schrödinger equation
3 to 4: Plug in our separation of xyz ansatz
4 to 5: Distribute out the RHS of the equation. Note that the d/dx derivative only acts on psi(x) not psi(y) or psi(z)
5 to 6: Divide both sides by psi(x) psi(y) psi(z). The total energy of the particle is constant
In equation 6, if the particle does not move in the x or y directions at all, the purple and blue terms are zero. This would mean that the green term, regardless of if I move in the z direction, is a constant. We can make the same argument for the purple and blue terms as well. Each colored term is just a constant.
Additionally, one might notice that the purple, blue, and green terms in equation 6 all independently look like the 1-dimensional Hamiltonian equation (for the x, y, and z dimension respectively). In 1-dimension they were also equal to their own constant. We can, just for simplicity, call this constant E_x, E_y, and E_z:
3: The 3-dimensional Schrödinger equation
3 to 4: Plug in our separation of xyz ansatz
4 to 5: Distribute out the RHS of the equation. Note that the d/dx derivative only acts on psi(x) not psi(y) or psi(z)
5 to 6: Divide both sides by psi(x) psi(y) psi(z). The total energy of the particle is constant
In equation 6, if the particle does not move in the x or y directions at all, the purple and blue terms are zero. This would mean that the green term, regardless of if I move in the z direction, is a constant. We can make the same argument for the purple and blue terms as well. Each colored term is just a constant.
Additionally, one might notice that the purple, blue, and green terms in equation 6 all independently look like the 1-dimensional Hamiltonian equation (for the x, y, and z dimension respectively). In 1-dimension they were also equal to their own constant. We can, just for simplicity, call this constant E_x, E_y, and E_z:
In order to make sure everyone is following, let us review some key steps below:
7: Take the constant 'E' and break it up into three different constants
We then separated out the constants into 3 different 1D equations (of which we have already solved). The steps to solve the equation is shown again for clarity. We now see that we have 3 different k values.
Now that we have solved each individual psi in its respective dimension, we can plug it back into our ansatz:
7: Take the constant 'E' and break it up into three different constants
We then separated out the constants into 3 different 1D equations (of which we have already solved). The steps to solve the equation is shown again for clarity. We now see that we have 3 different k values.
Now that we have solved each individual psi in its respective dimension, we can plug it back into our ansatz:
|
|
|