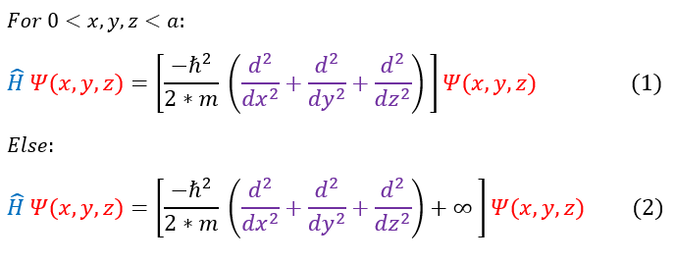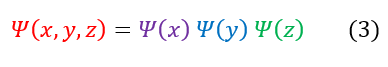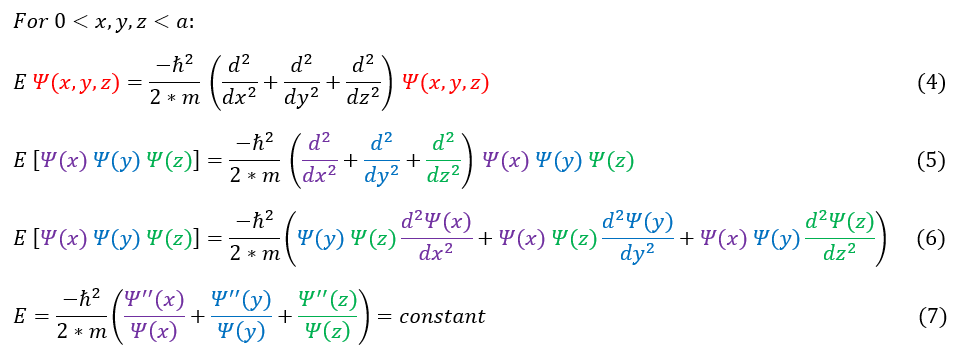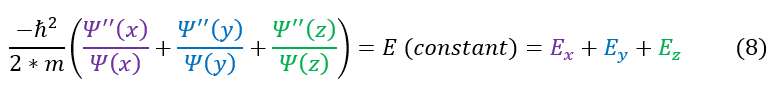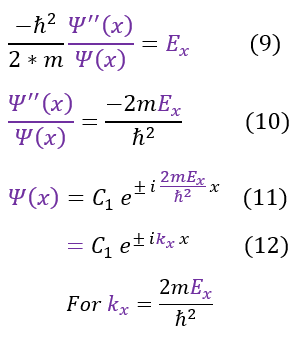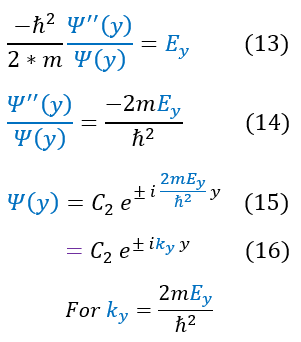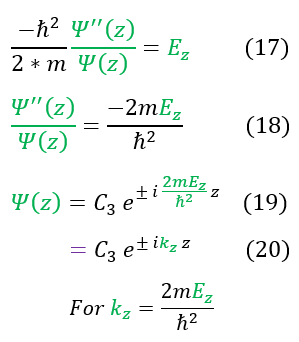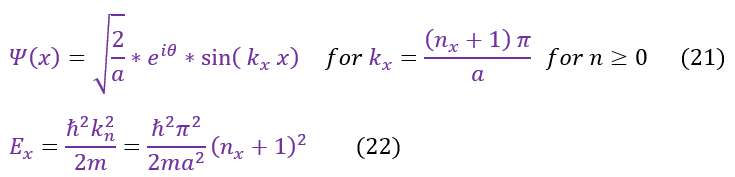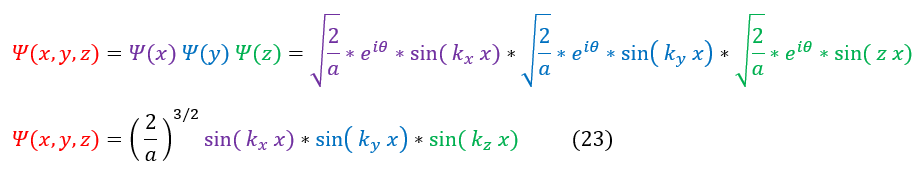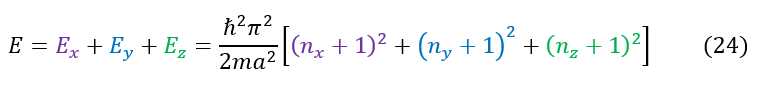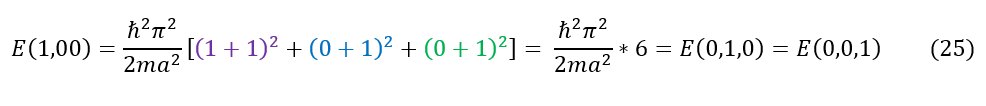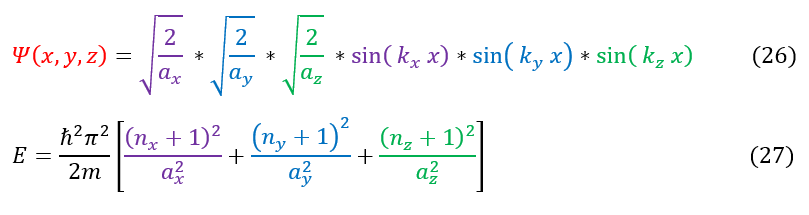Mind Network - Samuel Solomon
Infinite Cubic Well
3D Particle in a Box
|
|
|
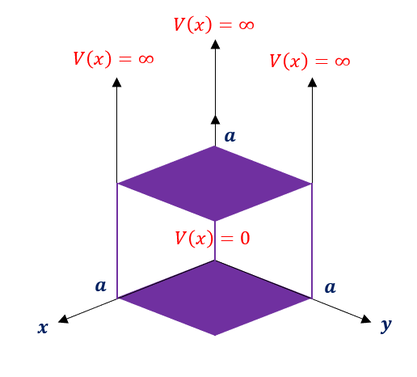
Now that we have redefined our Schrödinger equation in 3 dimensions, let us see how this effects the particle in a box (infinite square well) problem we solved earlier. The 2D square well will now turn into a 3D cube with side lengths of 'a.' For a visual, the potential energy diagram will look as follows:
Everywhere inside the well, the potential is equal to zero (like a free particle). Everywhere outside the well, the potential energy is equal to infinity. Our 3 dimensional Schrödinger equation will look like:
Going back to the infinite square well example, we have already discussed that NO wave function can solve equation 2 (as we have an infinity term). The only way for this to hold is if psi(x) = 0 outside the well. To solve the inside of the well, we are going to make our separation of variables approximation for a standing wave (just like we did for the free particle):
We are now in a position to solve the Schrödinger equation in equation 1:Schrödinger
In order to make sure everyone is following, let us review some key steps below:
4: The 3-dimensional Schrödinger equation
4 to 5: Plug in our separation of xyz ansatz
5 to 6: Distribute out the RHS of the equation. Note that the d/dx derivative only acts on psi(x) not psi(y) or psi(z)
6 to 7: Divide both sides by psi(x) psi(y) psi(z). The total energy of the particle is constant
In equation 7, if the particle does not move in the x or y directions at all, the purple and blue terms are zero. This would mean that the green term, regardless of if I move in the z direction, is a constant. We can make the same argument for the purple and blue terms as well. Each colored term is just a constant.
Additionally, one might notice that the purple, blue, and green terms in equation 6 all independently look like the 1-dimensional Hamiltonian equation (for the x, y, and z dimension respectively). In 1-dimension they were also equal to their own constant. We can, just for simplicity, call this constant E_x, E_y, and E_z:
4: The 3-dimensional Schrödinger equation
4 to 5: Plug in our separation of xyz ansatz
5 to 6: Distribute out the RHS of the equation. Note that the d/dx derivative only acts on psi(x) not psi(y) or psi(z)
6 to 7: Divide both sides by psi(x) psi(y) psi(z). The total energy of the particle is constant
In equation 7, if the particle does not move in the x or y directions at all, the purple and blue terms are zero. This would mean that the green term, regardless of if I move in the z direction, is a constant. We can make the same argument for the purple and blue terms as well. Each colored term is just a constant.
Additionally, one might notice that the purple, blue, and green terms in equation 6 all independently look like the 1-dimensional Hamiltonian equation (for the x, y, and z dimension respectively). In 1-dimension they were also equal to their own constant. We can, just for simplicity, call this constant E_x, E_y, and E_z:
In order to make sure everyone is following, let us review some key steps below:
7: Take the constant 'E' and break it up into three different constants
We then separated out the constants into 3 different 1D equations (of which we have already solved). The steps to solve the equation is shown again for clarity. We now see that we have 3 different k values.
Our equations, for now, match that of a free particle. The one caveat is that this is only part of the solution. We still need to patch it to the second half (where the potential is infinity; outside the box). To do this we will employ our two boundary conditions for a wave:
1. No matter the potential, the wave function must be continuous
2. The slope of the wave function is only continuous for a finite potential barrier
Obviously the potential barrier is an infinite barrier, so our wave function's slope is not continuous (with an ill-defined jump condition). Nonetheless, we can apply the boundary condition that all around the edges of the box, our wave functions must match inside and outside of the box. it is zero on the outside, so it must be zero on the edges as well. We have previously solved this in the 1-domensional case and found:
7: Take the constant 'E' and break it up into three different constants
We then separated out the constants into 3 different 1D equations (of which we have already solved). The steps to solve the equation is shown again for clarity. We now see that we have 3 different k values.
Our equations, for now, match that of a free particle. The one caveat is that this is only part of the solution. We still need to patch it to the second half (where the potential is infinity; outside the box). To do this we will employ our two boundary conditions for a wave:
1. No matter the potential, the wave function must be continuous
2. The slope of the wave function is only continuous for a finite potential barrier
Obviously the potential barrier is an infinite barrier, so our wave function's slope is not continuous (with an ill-defined jump condition). Nonetheless, we can apply the boundary condition that all around the edges of the box, our wave functions must match inside and outside of the box. it is zero on the outside, so it must be zero on the edges as well. We have previously solved this in the 1-domensional case and found:
Now that we have solved each individual psi in its respective dimension, we can plug it back into our ansatz:
We can also add up all the individual energies to find the total energy:
It is important to now realize that, unlike in 1-dimension, in 3-dimensions we CAN have degenerates states. An example of this can be seen below:
The only way to break the degeneracy is to break the symmetry of the problem (ie make it an infinite rectangular prism instead). If the side lengths of the cube all have different values than the equations reduce to the forms below:
|
|
|