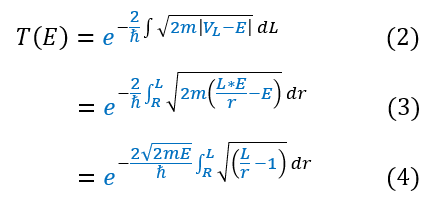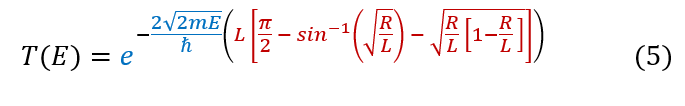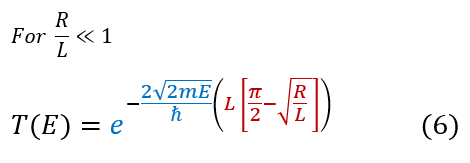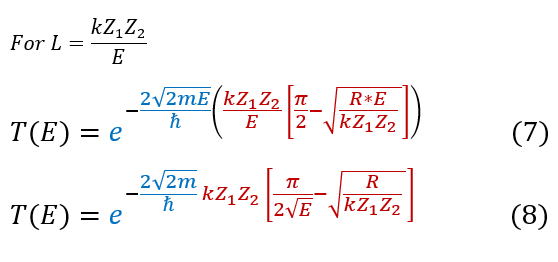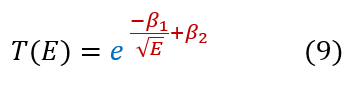Mind Network - Samuel Solomon
Quantum Tunneling
Alpha Decay Example
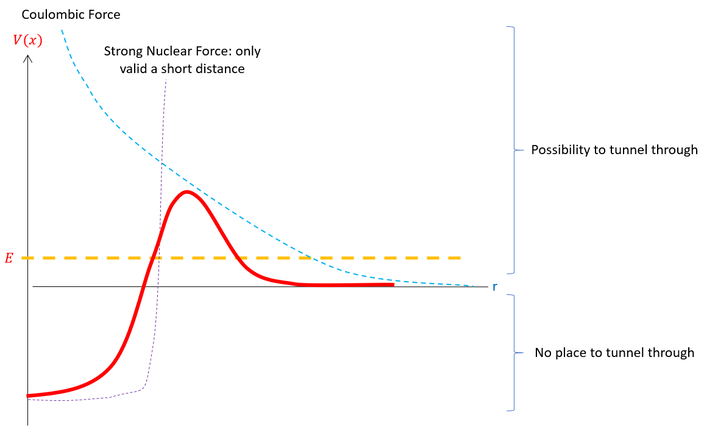
Circling back to the introduction of tunneling, I previously stated that scientists can use quantum tunneling principles to push reactions forwards that would otherwise, classically, not have enough energy to precede. One example of this occurring in nature is the alpha decay process. The potential diagram for the alpha decay is as follow:
Okay, the above picture might be a bit intimidating so lets break it down:
Purple dotted line: The strong force holding the nucleus together (short range: only for close distances to nucleus)
Blue dotted line: The coulombic force that the nucleus exerts at all distances (exponential decay of 1/r^2)
Red straight line: The combination of the two energies (Force *distance = energy)
Notice that the strong nuclear force dominates early (but does NOT contribute at all very far away from the nucleus although it seems to diverge to infinity).
Physically, the picture represents the energy barrier an alpha particle would feel leaving the nucleus. Think of it as a reaction barrier. The decay may be thermodynamically stable for heavy nuclei, but there is still an activation energy to jump over for the reaction to proceed. It turns out that the energy needed for the particle to decay out of the nucleus is generally GREATER than the energy of the particle. In fact, alpha decay is an inherent quantum tunneling phenomenon (would not exist without quantum tunneling).
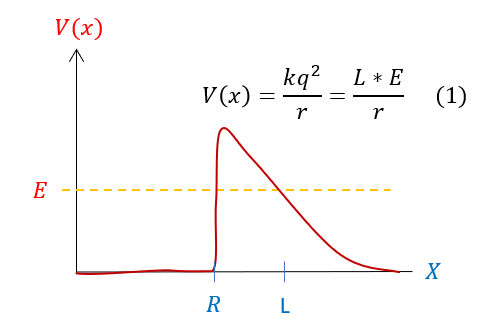
Let us now begin evaluating this problem. We notice that for certain energies, there is NO possibility of the alpha particle tunneling out of the nucleus. In this motivation, we will make a simplifying approximation to the potential shown below:
Purple dotted line: The strong force holding the nucleus together (short range: only for close distances to nucleus)
Blue dotted line: The coulombic force that the nucleus exerts at all distances (exponential decay of 1/r^2)
Red straight line: The combination of the two energies (Force *distance = energy)
Notice that the strong nuclear force dominates early (but does NOT contribute at all very far away from the nucleus although it seems to diverge to infinity).
Physically, the picture represents the energy barrier an alpha particle would feel leaving the nucleus. Think of it as a reaction barrier. The decay may be thermodynamically stable for heavy nuclei, but there is still an activation energy to jump over for the reaction to proceed. It turns out that the energy needed for the particle to decay out of the nucleus is generally GREATER than the energy of the particle. In fact, alpha decay is an inherent quantum tunneling phenomenon (would not exist without quantum tunneling).
Let us now begin evaluating this problem. We notice that for certain energies, there is NO possibility of the alpha particle tunneling out of the nucleus. In this motivation, we will make a simplifying approximation to the potential shown below:
To be clear: we are only analyzing the portion of the potential that the energy tunnels through. Specifically, this corresponds to the coulombic potential portion, which means for now we will ignore the strong force. The radius at which the coulombic potential matters is the radius of the nucleus itself (the strong force only exists inside the nucleus). Hence we will define 'R' as the nucleus's radius. To be clear: this is an approximation to the problem at hand, but a reasonable one.
We can now bring back out total transmission coefficient found in the last page (for large energy-potential gaps like this one):
We can now bring back out total transmission coefficient found in the last page (for large energy-potential gaps like this one):
In order to make sure everyone is following, let us review some key steps below:
2: Our previous formula for the total transmission coefficient
2 to 3: Plug in our integral bound and V(x) equation
3 to 4: Factor out the constant sqrt(2mE)
With the invention of computational online tools, one never need to get bogged down in long integrals. We can solve the integral online to yield the final equation below:
2: Our previous formula for the total transmission coefficient
2 to 3: Plug in our integral bound and V(x) equation
3 to 4: Factor out the constant sqrt(2mE)
With the invention of computational online tools, one never need to get bogged down in long integrals. We can solve the integral online to yield the final equation below:
The radius 'R' of a nucleus is actually EXTREMELY small. We can therefore make the approximation:
'L' actually relates to the particles energy. We can substitute its full expression back in:
And that is alpha decay. Now we did make some approximation for the sake of this problem; however, in general, people find alpha decay as:
With beta_1 and beta_2 both constants that relate to the Z (number of protons) of the nucleus. While our expression in equation 8 is NOT the exact expression for alpha decay, we did find the correct energy dependence of the system and only off by some constants in the exponent (taking a rigorous look at all the potentials the alpha particle faces will get you a better answer).