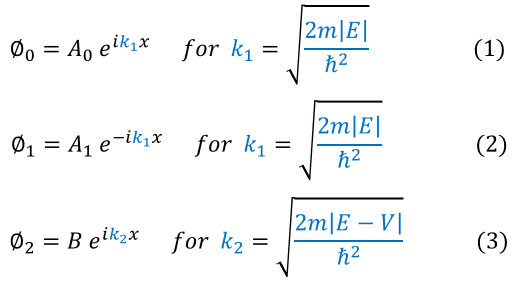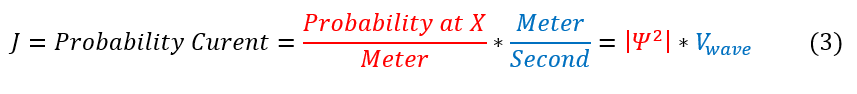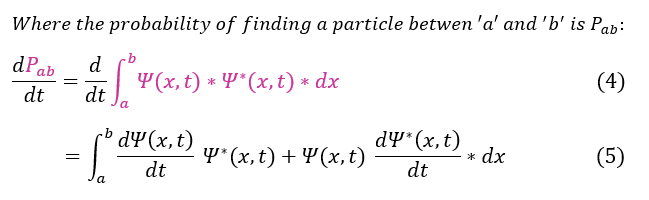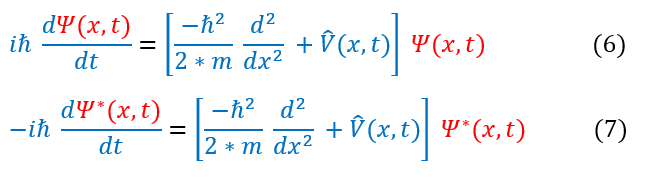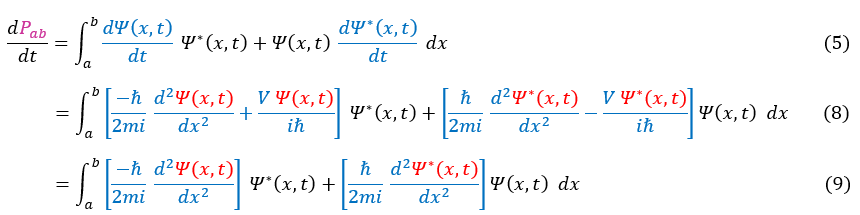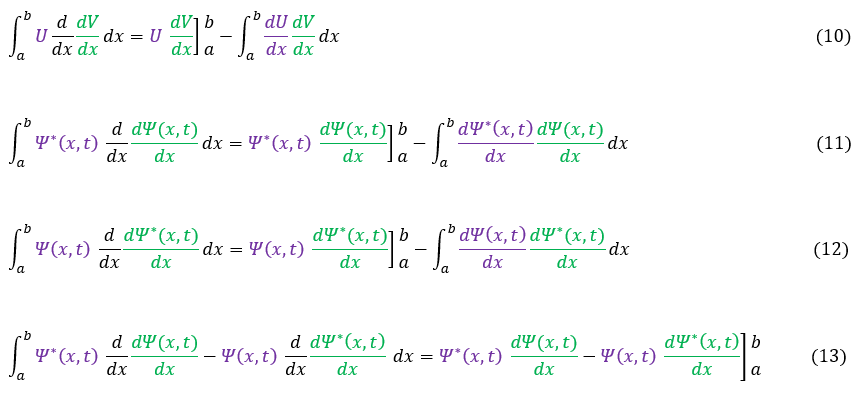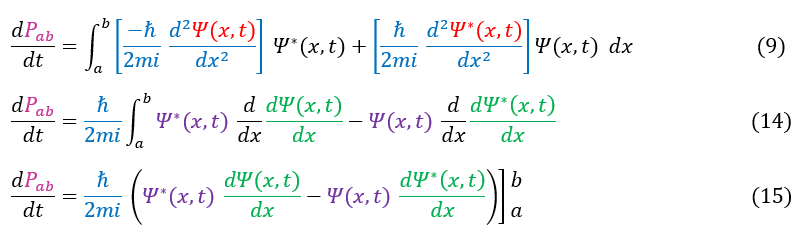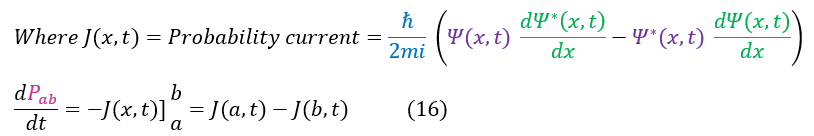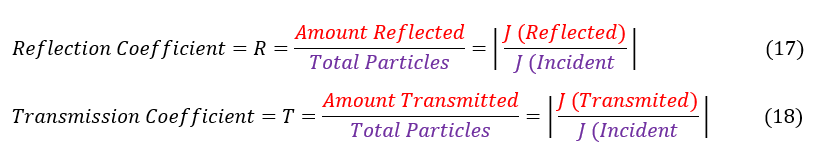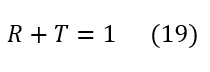Mind Network - Samuel Solomon
Scatter States
Reflection, Transmission, Probability Current
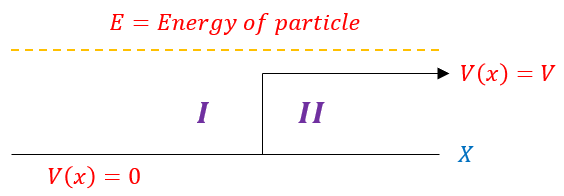
Let us consider a simple example. Two waves hit a barrier. One has enough energy to surmount the barrier, while one does not. Classically, one would expect the high energy wave to surmount the barrier and the low energy wave to bounce back. While the quantum situation may not exactly follow the classical picture (there is tunneling and scattering), we wold lose generality if we dd not consider the possibility for the wave to be reflected and transmitted over the barrier.
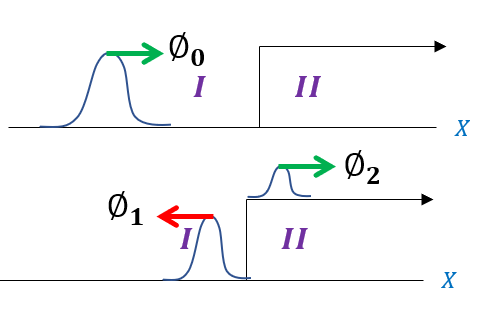
We represent one wave function as the sum of its infinitesimal basis waves. Therefore, even when one wave function encounters a barrier, with enough energy to surmount it, the basis waves interact with that barrier in a variety of different waves (based on their energies). The waves disperse and some are reflected and some are transmitted. To be clear, the before and after picture (time evolved situation) appears as follows:
We represent one wave function as the sum of its infinitesimal basis waves. Therefore, even when one wave function encounters a barrier, with enough energy to surmount it, the basis waves interact with that barrier in a variety of different waves (based on their energies). The waves disperse and some are reflected and some are transmitted. To be clear, the before and after picture (time evolved situation) appears as follows:
Because the area under the wave function (phi_0) is ALWAYS one (must be normalized), we know that the fractions of the reflected (phi_1) and transmitted (phi_2) waves have an area that also sums to one. We know this is true because the amplitude of the wave function relates to the probability of finding a particle in that location. Experimentally, we see this because we would expect the fraction of particles measured at a given location to be the amplitude squared. Hence, the area relates to the number of particles present, and as the wave splits we do NOT loose any particles (very specific cases may, but that's more nuclear engineering).
In summation, the total area of the reflected and transmitted wave must still add up to one. They are only fractions of the initial wave. Let us mathematically represent the waves before and after the barrier (it is just a particle in a box where the whole system is classically allowed) as:
In summation, the total area of the reflected and transmitted wave must still add up to one. They are only fractions of the initial wave. Let us mathematically represent the waves before and after the barrier (it is just a particle in a box where the whole system is classically allowed) as:
In order to make sure everyone is following, let us review some key steps below:
1: Phi_0 is moving in the positive x direction with an energy-potential gap of E
2: Phi_1 is moving in the negative x direction with an energy-potential gap of E
3: Phi_2 is moving in the positive x direction with an energy-potential gap of E - V
The direction of propagation is represented by the +/- ikx. We are simply using a plane wave propagating for now (note the time component is being ignored for now, but can easily be added in).
So the physics question is: what changes in the waves? The answer: only the coefficient in front. The ikx term in the e^ikx is fixed based on the energy-potential gap. It has nothing to do with whether or not the wave was reflected or transmitted!! What does change is the amplitude coefficient (which we predicted as that relates to the number of particles). We can therefore find how much of the wave is transmitted or reflected based on the coefficient in front of the amplitude (the variable that is effected). We know that the total area of the initial wave is just split into the reflected and transmitted ones; hence, B and A_1 are really just fractions of the initial A_0 amplitude. We call the fraction amount the reflection and transmission coefficients:
1: Phi_0 is moving in the positive x direction with an energy-potential gap of E
2: Phi_1 is moving in the negative x direction with an energy-potential gap of E
3: Phi_2 is moving in the positive x direction with an energy-potential gap of E - V
The direction of propagation is represented by the +/- ikx. We are simply using a plane wave propagating for now (note the time component is being ignored for now, but can easily be added in).
So the physics question is: what changes in the waves? The answer: only the coefficient in front. The ikx term in the e^ikx is fixed based on the energy-potential gap. It has nothing to do with whether or not the wave was reflected or transmitted!! What does change is the amplitude coefficient (which we predicted as that relates to the number of particles). We can therefore find how much of the wave is transmitted or reflected based on the coefficient in front of the amplitude (the variable that is effected). We know that the total area of the initial wave is just split into the reflected and transmitted ones; hence, B and A_1 are really just fractions of the initial A_0 amplitude. We call the fraction amount the reflection and transmission coefficients:
In order to make sure everyone is following: the amount of particles present in the initial, reflected, or transmitted wave relates to the amplitude squared present (the probability of a particle in that location is psi^2). However, psi^2 is not a constant in every location as the wave is moving (it is being time evolved). This complicates things.
We take psi^2/sec at a given x location to be the amount of particles moving into or out of the x location for a given time measured. As we take the limit of the measurement time to zero, we get the probability's velocity. We will call this the Probability Current and label it as J:
We take psi^2/sec at a given x location to be the amount of particles moving into or out of the x location for a given time measured. As we take the limit of the measurement time to zero, we get the probability's velocity. We will call this the Probability Current and label it as J:
While the equation above works for a plane wave, not all waves are so simple to describe (waves disperse or oscillate). A more general formula seen for the probability current is the 'continuity equation' derived in a few steps below:
In order to make sure everyone is following, let us review some key steps below:
4: Time derivative of the probability (probability current definition). Specifically evaluated from a to b
4 to 5: Bring the time derivative inside the space derivative and apply the chain rule
We now need to find a general value for the time derivative of the wave function. The only formula that contains this is the Schrödinger equation.
4: Time derivative of the probability (probability current definition). Specifically evaluated from a to b
4 to 5: Bring the time derivative inside the space derivative and apply the chain rule
We now need to find a general value for the time derivative of the wave function. The only formula that contains this is the Schrödinger equation.
In order to make sure everyone is following, let us review some key steps below:
6: The Schrödinger equation
6 to 7: The complex conjugate of equation 6
Let us now plug this back into equation 5:
6: The Schrödinger equation
6 to 7: The complex conjugate of equation 6
Let us now plug this back into equation 5:
In order to make sure everyone is following, let us review some key steps below:
8: Replace dpsi/dt and dpsi*/dt with their corresponding form from the Schrödinger equation
9: Cross out the potential terms as they cancel
To solve the remaining term, we must use integration by parts (the integral of the product rule):
8: Replace dpsi/dt and dpsi*/dt with their corresponding form from the Schrödinger equation
9: Cross out the potential terms as they cancel
To solve the remaining term, we must use integration by parts (the integral of the product rule):
In order to make sure everyone is following, let us review some key steps below:
10: Integration by parts formula
11 and 12: Apply integration by parts
13: Equation 11 minus equation 12
Now plug equation 13 back into equation 9:
10: Integration by parts formula
11 and 12: Apply integration by parts
13: Equation 11 minus equation 12
Now plug equation 13 back into equation 9:
In order to make sure everyone is following, let us review some key steps below:
14: Simplify equation 9 as to look like equation 13
14 to 15: Plug in the results from integration by parts (see equation 13)
Equation 15 is called the continuity equation. As we were solving for probability current, we can now add a definition of the probability current as follows:
14: Simplify equation 9 as to look like equation 13
14 to 15: Plug in the results from integration by parts (see equation 13)
Equation 15 is called the continuity equation. As we were solving for probability current, we can now add a definition of the probability current as follows:
We can now define our transmission and reflection coefficients in terms of the probability current J:
One last important piece to remember is that we only really need to solve for one of the coefficients above as the sum of the two waves must equal the initial wave. Hence, the sum of the fractional split must equal one:
|
|
|